题目内容
已知实数x，y满足条件
，若目标函数z=mx-y（m≠0）取得最大值时的最优解有无穷多个，则实数m值为（ ）
|
| A、1 | ||
B、
| ||
C、-
| ||
| D、-1 |
考点：简单线性规划
专题：数形结合,不等式的解法及应用
分析：由约束条件作出可行域，化目标函数为直线方程的斜截式，结合已知目标函数z=mx-y（m≠0）取得最大值时的最优解有无穷多个可求得m的值．
解答：
解：由约束条件
作出可行域如图，
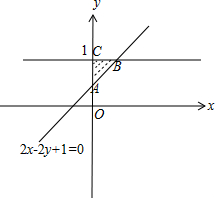
化目标函数z=mx-y为y=mx-z，
∵目标函数z=mx-y（m≠0）取得最大值时的最优解有无穷多个，
∴m=1．
故选：A．
|
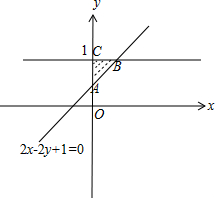
化目标函数z=mx-y为y=mx-z，
∵目标函数z=mx-y（m≠0）取得最大值时的最优解有无穷多个，
∴m=1．
故选：A．
点评：本题考查了简单的线性规划，考查了数形结合的解题思想方法，是中档题．
练习册系列答案
新课标阶梯阅读训练系列答案
相关题目
从6人中选4人分别到省内黄果树、小七孔、西江苗寨、梵净山游览，要求每个地点有一人游览，每人只游览一个地点，且在这6人中甲、乙不去西江苗寨游览，则不同的选择方案共有（ ）
| A、300种 | B、240种 |
| C、144种 | D、96种 |
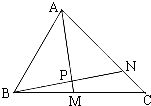如图所示，在△ABC中，点M是BC的中点，点N在AC上，且AN=2NC，AM与BN交于点P，求AP：PM与BP：PN的值．