题目内容
已知:在空间四边形ABCS中,AC=AS,BC=BS,求证:AB⊥CS.


考点:空间中直线与直线之间的位置关系
专题:空间位置关系与距离
分析:取SC中点O,连结BO,AO,由已知条件推导出SC⊥平面ABO,由此能证明AB⊥CS.
解答:
证明:取SC中点O,连结BO,AO,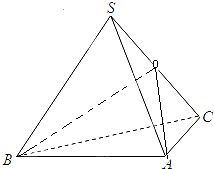
∵AC=AS,BC=BS,
∴AO⊥SC,BO⊥SC,
又AO∩BO=O,
∴SC⊥平面ABO,
∵AB?平面ABO,
∴AB⊥CS.

∵AC=AS,BC=BS,
∴AO⊥SC,BO⊥SC,
又AO∩BO=O,
∴SC⊥平面ABO,
∵AB?平面ABO,
∴AB⊥CS.
点评:本题考查异面直线垂直的证明,是基础题,解题时要注意空间思维能力的培养.

练习册系列答案
相关题目
在曲线f(x)=x3+3x2+6x-10的切线中,斜率最小的切线方程为( )
| A、x-3y+6=0 |
| B、x+3y-11=0 |
| C、3x+y+11=0 |
| D、3x-y-12=0 |
已知实数x,y满足条件
,若目标函数z=mx-y(m≠0)取得最大值时的最优解有无穷多个,则实数m值为( )
|
| A、1 | ||
B、
| ||
C、-
| ||
| D、-1 |
抛物线y=3x2的焦点坐标是( )
A、(
| ||
B、(0,
| ||
C、(
| ||
D、(0,
|
设a=0.50.5,b=0.30.5,c=log0.32,则a,b,c的大小关系是( )
| A、a>b>c |
| B、a<b<c |
| C、b<a<c |
| D、a<c<b |