题目内容
(本小题满分14分)己知函数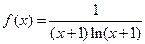 .
.
(1) 求函数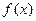 的定义域;(2) 求函数
的定义域;(2) 求函数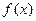 的增区间;
的增区间;
(3) 是否存在实数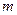 ,使不等式
,使不等式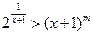 在
在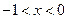 时恒成立?若存在,求出实数
时恒成立?若存在,求出实数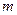 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
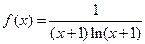 .
.(1) 求函数
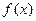 的定义域;(2) 求函数
的定义域;(2) 求函数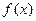 的增区间;
的增区间;(3) 是否存在实数
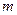 ,使不等式
,使不等式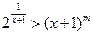 在
在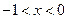 时恒成立?若存在,求出实数
时恒成立?若存在,求出实数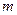 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.:(1)根据函数解析式得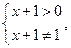
解得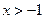 且
且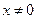 .
.
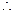 函数
函数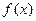 的定义域是
的定义域是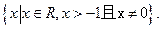 …………3分
…………3分
(2)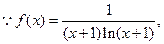
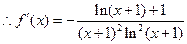 ……………………5分
……………………5分
由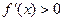 得
得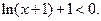
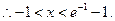
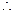 函数
函数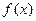 的增区间为
的增区间为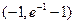 . …………………………8分
. …………………………8分
(3)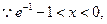
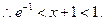
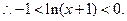
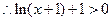
 当
当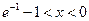 时,
时,
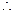 在区间
在区间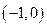 上,
上,
当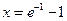 时,
时,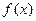 取得最大值.
取得最大值.
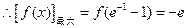 .……………………………10分
.……………………………10分
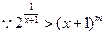 在
在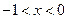 时恒成立.
时恒成立.
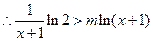 在
在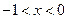 时恒成立.
时恒成立.
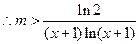 在
在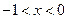 时恒成立.
时恒成立.
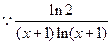 在
在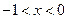 时的最大值等于
时的最大值等于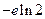 .
.
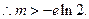
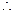 当
当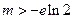 时,不等式
时,不等式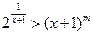 在
在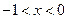
时恒成立.……… 14分
14分
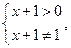
解得
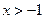 且
且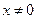 .
.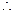 函数
函数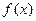 的定义域是
的定义域是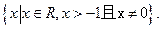 …………3分
…………3分(2)
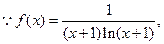
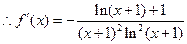 ……………………5分
……………………5分由
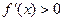 得
得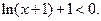
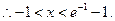
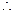 函数
函数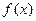 的增区间为
的增区间为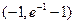 . …………………………8分
. …………………………8分(3)
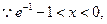
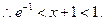
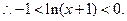
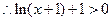
 当
当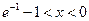 时,
时,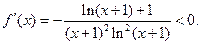
 在区间
在区间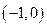 上,
上, 当
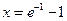 时,
时,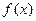 取得最大值.
取得最大值.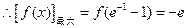 .……………………………10分
.……………………………10分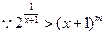 在
在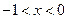 时恒成立.
时恒成立.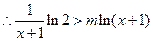 在
在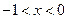 时恒成立.
时恒成立.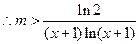 在
在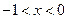 时恒成立.
时恒成立.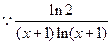 在
在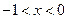 时的最大值等于
时的最大值等于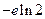 .
.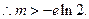
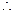 当
当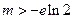 时,不等式
时,不等式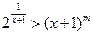 在
在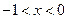
时恒成立.………
 14分
14分略

练习册系列答案
相关题目
 在一直线上运动,在此直线上与物体A出发的同时,物体B在物体A的正前方5m处以
在一直线上运动,在此直线上与物体A出发的同时,物体B在物体A的正前方5m处以 的速度与A同向运动,问两物体何时相遇?相遇时物体A的走过的路程是多少?(时间单位为:s,速度单位为:m/s)
的速度与A同向运动,问两物体何时相遇?相遇时物体A的走过的路程是多少?(时间单位为:s,速度单位为:m/s) 要在公园内建一块顶点都在圆P上的多边形活动场地.
要在公园内建一块顶点都在圆P上的多边形活动场地.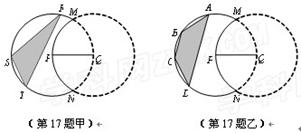
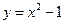 ,直线
,直线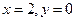 所围成的图形的面积
所围成的图形的面积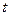 元(
元(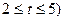 ,设该食品厂每公斤蘑菇的出厂价为
,设该食品厂每公斤蘑菇的出厂价为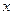 元(
元(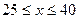 ),根据
),根据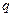 与
与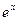 成反比,当每
成反比,当每 公斤蘑菇的出厂价为30元时,日销售量为100公斤.
公斤蘑菇的出厂价为30元时,日销售量为100公斤.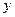 元与每公斤蘑菇的出厂价
元与每公斤蘑菇的出厂价 ,当每公斤蘑菇的出厂价
,当每公斤蘑菇的出厂价 最大,并求最大值
最大,并求最大值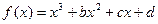 的图像过点
的图像过点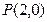 ,且在点
,且在点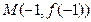 处的切线方程为
处的切线方程为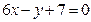 .
.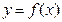 的解析式;
的解析式;  ,若函数
,若函数 有大于零的极值点,则( )
有大于零的极值点,则( )



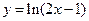 上的点到直线
上的点到直线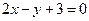 的最短距离是 .
的最短距离是 .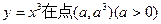 处的切线与x轴、直线
处的切线与x轴、直线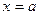 所围成的三角形的面积为
所围成的三角形的面积为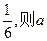 = .
= .