题目内容
4. 已知正四棱锥P-ABCD中,AB=6cm,侧面与底面ABCD所成角的大小为45°
已知正四棱锥P-ABCD中,AB=6cm,侧面与底面ABCD所成角的大小为45°(1)求正四棱锥的体积;
(2)侧棱与底面所成角的大小(精确到1度)
分析 (1)求四棱锥P-ABCD的体积,关键是求出底面积与高,进而利用公式求解.
(2)要求侧棱与底面ABCD所成角的大小,关键是找出侧棱在底面ABCD上的射影.找出所求角的平面角,进而可求侧棱与底面ABCD所成角的大小.
解答  解:(1)过P作斜高PE,PO⊥底面ABCD,AD∥BC.
解:(1)过P作斜高PE,PO⊥底面ABCD,AD∥BC.
正四棱锥P-ABCD中,AB=6cm,侧面与底面ABCD所成角的大小为45°,即∠PEO=45°,PO=3.
VP-ABCD=$\frac{1}{3}×6×6×3$=36.(cm3).
(2)连结OB,PO⊥底面ABCD,∠PBO就是侧棱与底面所成角.侧棱与底面ABCD所成角的大小为:θ.
OB=3$\sqrt{2}$.
tanθ=$\frac{3}{3\sqrt{2}}$=$\frac{\sqrt{2}}{2}$.
可得θ=36°.
点评 本题的考点是直线与平面所成的角,主要考查侧棱与底面ABCD所成角的大小,关键是找出侧棱在底面ABCD上的射影,考查几何体的体积,属于中档题.

练习册系列答案
相关题目
14.某商店计划每天购进某商品若干件,商店每销售一件该商品可获利润50元,若供大于求,剩余商品全部退回,但每件商品亏损10元;若供不应求,则从外部调剂,此时每件调剂商品可获利润30元
(1)若商店一天购进该商品10件,求当天的利润y(单位:元)关于当天需求量n(单位:件,n∈N)的函数解析式
(2)商店记录了50天该商品的日需求量n(单位:件)整理得表:
若商店一天购进10件该商品,以50天记录的各需求量发生的概率,求当天的利润在区间[400,500]的概率.
(1)若商店一天购进该商品10件,求当天的利润y(单位:元)关于当天需求量n(单位:件,n∈N)的函数解析式
(2)商店记录了50天该商品的日需求量n(单位:件)整理得表:
| 日需求量 | 8 | 9 | 10 | 11 | 12 |
| 频数 | 9 | 11 | 15 | 10 | 5 |
12.已知集合A={x|3x-x2>0},B={0,1,2,3},则A∩B等于( )
| A. | {0,1} | B. | {1,2} | C. | {1,2,3} | D. | {0,1,2,3} |
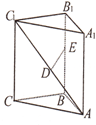 如图,直三棱柱ABC一A1B1C1中,AB=$\sqrt{2}$,AC=3,BC=$\sqrt{5}$,D是ACl的中点,E是侧棱BB1上的一个动点
如图,直三棱柱ABC一A1B1C1中,AB=$\sqrt{2}$,AC=3,BC=$\sqrt{5}$,D是ACl的中点,E是侧棱BB1上的一个动点