题目内容
14.已知函数f(x)=cos(-$\frac{x}{2}$)+sin($π-\frac{x}{2}$),x∈R.(1)求函数f(x)的最小正周期;
(2)当x∈[-90,90],求函数f(x)的最值;
(3)求f(x)在[0,180)上的减区间.
分析 (1)由三角函数中的恒等变换应用化简函数解析式可得f(x)=$\sqrt{2}$sin($\frac{x}{2}$+45°),由周期公式即可得解.
(2)由x∈[-90°,90°]解得$\frac{x}{2}$+45°的范围,可求sin($\frac{x}{2}$+45°)的范围,即可求得函数f(x)的最值.
(3)由x∈[0°,180°),可求$\frac{x}{2}$+45°的范围,根据正弦函数的图象和性质即可求的f(x)在[0,180)上的减区间.
解答 解:(1)∵f(x)=cos(-$\frac{x}{2}$)+sin($π-\frac{x}{2}$)=cos($\frac{x}{2}$)+sin($\frac{x}{2}$)=$\sqrt{2}$sin($\frac{x}{2}$+45°),
∴函数f(x)的最小正周期T=$\frac{2π}{\frac{1}{2}}$=4π.
(2)∵x∈[-90°,90°],
∴$\frac{x}{2}$∈[-45°,45°],$\frac{x}{2}$+45°∈[0,90°],
∴sin($\frac{x}{2}$+45°)∈[0,1],
∴函数f(x)=$\sqrt{2}$sin($\frac{x}{2}$+45°)的最大值为$\sqrt{2}$,最小值为0.
(3)∵x∈[0°,180°),
∴$\frac{x}{2}$∈[0,90°),$\frac{x}{2}$+45°∈[45°,135°),
∴f(x)=$\sqrt{2}$sin($\frac{x}{2}$+45°)在[0,180)上的减区间为:[90°,180°).
点评 本题主要考查了三角函数中的恒等变换应用,余弦函数的图象和性质,属于基本知识的考查.

练习册系列答案
相关题目
3.某几何体的三视图如图所示,则该几何体的体积是( )


| A. | 2 | B. | $\frac{8}{3}$ | C. | 4 | D. | $\frac{20}{9}$ |
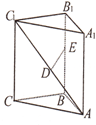 如图,直三棱柱ABC一A1B1C1中,AB=$\sqrt{2}$,AC=3,BC=$\sqrt{5}$,D是ACl的中点,E是侧棱BB1上的一个动点
如图,直三棱柱ABC一A1B1C1中,AB=$\sqrt{2}$,AC=3,BC=$\sqrt{5}$,D是ACl的中点,E是侧棱BB1上的一个动点