题目内容
1.已知函数f(x)=ax+xlnx的图象在点x=e(e为自然对数的底数)处的切线斜率为3.(1)求实数a的值;
(2)若存在x0>1,满足f(x0)-k(x0-1)<0,求整数k的最大值.
分析 (1)求出f(x)的导函数,把x=e代入导函数中求出的导函数值即为切线方程的斜率,根据切线斜率为3列出关于a的方程,求出方程的解即可得到a的值;
(2)将原来的恒成立问题转化为研究函数的最值问题,研究g(x)=$\frac{x+xlnx}{x-1}$区间(1,+∞)上的最值问题,先求出函数的极值,研究极值点左右的单调性,最后确定出最小值,从而得出k的最大值.
解答 解:(1)因为f(x)=ax+xlnx,
所以f′(x)=a+lnx+1.
因为函数f(x)=ax+xlnx的图象在点x=e处的切线斜率为3,
所以f′(e)=3,即a+lne+1=3.
所以a=1.
(2)由(1)知,f(x)=x+xlnx,
所以不等式k(x-1)<f(x)在x∈(1,+∞)上恒成立,
即k<$\frac{x+xlnx}{x-1}$对任意x>1恒成立.
令g(x)=$\frac{x+xlnx}{x-1}$,
则g′(x)=$\frac{x-lnx-2}{(x-1)^{2}}$,
令h(x)=x-lnx-2(x>1),
则h′(x)=1-$\frac{1}{x}$=$\frac{x-1}{x}$>0在(1,+∞)上恒成立,
所以函数h(x)在(1,+∞)上单调递增.
因为h(3)=1-ln3<0,h(4)=2-2ln2>0,
所以方程h(x)=0在(1,+∞)上存在唯一实根x0,且满足x0∈(3,4).
当1<x<x0时,h(x)<0,即g'(x)<0,当x>x0时,h(x)>0,即g'(x)>0,
所以函数g(x)=$\frac{x+xlnx}{x-1}$在(1,x0)上单调递减,在(x0,+∞)上单调递增.
所以[g(x)]min=g(x0)=$\frac{{x}_{0}+{x}_{0}ln{x}_{0}}{{x}_{0}-1}$=$\frac{{x}_{0}(1+{x}_{0}-2)}{{x}_{0}-1}$=x0∈(3,4).
所以k<[g(x)]min=x0∈(3,4).
故整数k的最大值是3.
点评 此题考查学生会利用导数求切线上过某点切线方程的斜率,会利用导函数的正负确定函数的单调区间,会利用导数研究函数的极值,掌握导数在最大值、最小值问题中的应用,是一道难题.

| A. | {0,1} | B. | {1,2} | C. | {1,2,3} | D. | {0,1,2,3} |
| A. | $\frac{3-4\sqrt{3}}{10}$ | B. | $\frac{3+4\sqrt{3}}{10}$ | C. | $\frac{4+3\sqrt{3}}{10}$ | D. | $\frac{4-3\sqrt{3}}{10}$ |

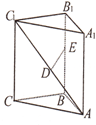 如图,直三棱柱ABC一A1B1C1中,AB=$\sqrt{2}$,AC=3,BC=$\sqrt{5}$,D是ACl的中点,E是侧棱BB1上的一个动点
如图,直三棱柱ABC一A1B1C1中,AB=$\sqrt{2}$,AC=3,BC=$\sqrt{5}$,D是ACl的中点,E是侧棱BB1上的一个动点