题目内容
18.函数f(x)=$\frac{\sqrt{6+x-{x}^{2}}}{lo{g}_{2}x-1}$的定义域用区间表示为[-2,2)∪(2,3].分析 根据函数成立的条件即可求函数的定义域.
解答 解:要使函数有意义,则$\left\{\begin{array}{l}{6+x-{x}^{2}≥0}\\{lo{g}_{2}x-1≠0}\end{array}\right.$,
即$\left\{\begin{array}{l}{-2≤x≤3}\\{x≠2}\end{array}\right.$,
即函数的定义域为[-2,2)∪(2,3],
故答案为:[-2,2)∪(2,3]
点评 本题主要考查函数的定义域的求解,要求熟练掌握常见函数成立的条件.

练习册系列答案
相关题目
8.在等腰梯形ABCD中,AB∥CD,且|AB|=2,|AD|=1,|CD|=2x其中x∈(0,1),以A,B为焦点且过点D的双曲线的离心率为e1,以C,D为焦点且过点A的椭圆的离心率为e2,若对任意x∈(0,1)不等式t<e1+e2恒成立,则t的最大值为( )
| A. | $\sqrt{3}$ | B. | $\sqrt{5}$ | C. | 2 | D. | $\sqrt{2}$ |
3.某几何体的三视图如图所示,则该几何体的体积是( )


| A. | 2 | B. | $\frac{8}{3}$ | C. | 4 | D. | $\frac{20}{9}$ |
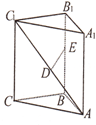 如图,直三棱柱ABC一A1B1C1中,AB=$\sqrt{2}$,AC=3,BC=$\sqrt{5}$,D是ACl的中点,E是侧棱BB1上的一个动点
如图,直三棱柱ABC一A1B1C1中,AB=$\sqrt{2}$,AC=3,BC=$\sqrt{5}$,D是ACl的中点,E是侧棱BB1上的一个动点