题目内容
19.设Sn为等差数列{an}的前n项和,且4Sn=n(an+an+1),a5=9.(1)求{an}的通项公式;
(2)设区间(an•2n,an+1•2n+1)内整数的个数为bn,令cn=$\frac{{b}_{n}-{2}^{n+2}+1}{{4}^{n}}$,若{cn}的前n项和为Tn,求证:Tn<3.
分析 (1)利用等差数列的通项公式及其前n项和公式即可得出;
(2)区间(an•2n,an+1•2n+1)即区间((2n-1)•2n,(2n+1)•2n+1),可得bn=(2n+3)•2n-1,cn=$\frac{2n-1}{{2}^{n}}$,再利用“错位相减法”、等比数列的前n项和公式即可得出.
解答 (1)解:设等差数列{an}的公差为d,
∵4Sn=n(an+an+1),
∴$4×\frac{n({a}_{1}+{a}_{n})}{2}$=n(an+an+1),
化为2a1=d,
又a5=9,∴a1+4d=9,
联立$\left\{\begin{array}{l}{2{a}_{1}=d}\\{{a}_{1}+4d=9}\end{array}\right.$,解得$\left\{\begin{array}{l}{{a}_{1}=1}\\{d=2}\end{array}\right.$.
∴an=1+2(n-1)=2n-1,
∴an=2n-1.
(2)证明:区间(an•2n,an+1•2n+1)即区间((2n-1)•2n,(2n+1)•2n+1),
∴bn=(2n+3)•2n-1,
∴cn=$\frac{{b}_{n}-{2}^{n+2}+1}{{4}^{n}}$=$\frac{2n-1}{{2}^{n}}$,
∴{cn}的前n项和为Tn=$\frac{1}{2}$+$\frac{3}{{2}^{2}}$+$\frac{5}{{2}^{3}}$+…+$\frac{2n-3}{{2}^{n-1}}$+$\frac{2n-1}{{2}^{n}}$,
$\frac{1}{2}{T}_{n}$=$\frac{1}{{2}^{2}}+\frac{3}{{2}^{3}}$+…+$\frac{2n-3}{{2}^{n}}$+$\frac{2n-1}{{2}^{n+1}}$,
∴$\frac{1}{2}{T}_{n}$=$\frac{1}{2}+\frac{2}{{2}^{2}}+\frac{2}{{2}^{3}}$+…+$\frac{2}{{2}^{n}}$-$\frac{2n-1}{{2}^{n+1}}$=$\frac{1}{2}+\frac{1}{2}+\frac{1}{{2}^{2}}$+…+$\frac{1}{{2}^{n-1}}$-$\frac{2n-1}{{2}^{n+1}}$=$\frac{1-\frac{1}{{2}^{n}}}{1-\frac{1}{2}}$-$\frac{1}{2}$-$\frac{2n-1}{{2}^{n+1}}$=$\frac{3}{2}$-$\frac{2n+1}{{2}^{n+1}}$,
∴Tn=$3-\frac{2n+1}{{2}^{n}}$.
∴Tn<3.
点评 本题考查了等差数列与等比数列的通项公式及其前n项和公式、“错位相减法”,考查了推理能力与计算能力,属于中档题.

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案(1)若商店一天购进该商品10件,求当天的利润y(单位:元)关于当天需求量n(单位:件,n∈N)的函数解析式
(2)商店记录了50天该商品的日需求量n(单位:件)整理得表:
| 日需求量 | 8 | 9 | 10 | 11 | 12 |
| 频数 | 9 | 11 | 15 | 10 | 5 |
| A. | $\sqrt{3}$ | B. | $\sqrt{5}$ | C. | 2 | D. | $\sqrt{2}$ |
 三棱柱ABC-A1B1C1中,CC1⊥平面ABC,△ABC是边长为4的等边三角形,D为AB边中点,且CC1=2AB.
三棱柱ABC-A1B1C1中,CC1⊥平面ABC,△ABC是边长为4的等边三角形,D为AB边中点,且CC1=2AB.

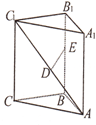 如图,直三棱柱ABC一A1B1C1中,AB=$\sqrt{2}$,AC=3,BC=$\sqrt{5}$,D是ACl的中点,E是侧棱BB1上的一个动点
如图,直三棱柱ABC一A1B1C1中,AB=$\sqrt{2}$,AC=3,BC=$\sqrt{5}$,D是ACl的中点,E是侧棱BB1上的一个动点