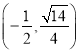Question

【题目】已知函数，若关于的不等式恰有3个整数解，则实数的最小值为（ ）

A. 1 B. C. D.

Answer 1

【答案】C

【解析】，等价于，即恰有个整数解，即有个整数解，，时，不等式无解，时，不等式只有一个整数解，排除选项，当时，由可得在递减，由可得在递增，，合题意，时，，不等式无解；，合题意，，合题意，当时，，不等式无解；故时，有且只有个整数解，又的最小值为，故选C.

【 方法点睛】本题主要考查分段函数的解析式、排除法解选择题，属于难题. 用特例代替题设所给的一般性条件，得出特殊结论，然后对各个选项进行检验，从而做出正确的判断，这种方法叫做特殊法. 若结果为定值，则可采用此法. 特殊法是“小题小做”的重要策略，排除法解答选择题是高中数学一种常见的解题思路和方法，这种方法即可以提高做题速度和效率，又能提高准确性，这种方法主要适合下列题型:(1)求值问题（可将选项逐个验证）；（2）求范围问题（可在选项中取特殊值，逐一排除）；（3）图象问题（可以用函数性质及特殊点排除）；（4）解方程、求解析式、求通项、求前 项和公式问题等等.