题目内容
8．计算（1）（2$\frac{1}{4}$）${\;}^{\frac{1}{2}}$-（-7.8）0-（3$\frac{3}{8}$）${\;}^{\frac{2}{3}}$+（$\frac{2}{3}$）-2
（2）（lg2）2+lg2•lg5+$\frac{lo{g}_{3}5}{lo{g}_{3}10}$．
分析 （1）利用有理指数幂的运算法则化简求解即可．
（2）利用导数的运算法则化简求解即可．
解答 （本小题满分10分）
解：（1）（2$\frac{1}{4}$）${\;}^{\frac{1}{2}}$-（-7.8）0-（3$\frac{3}{8}$）${\;}^{\frac{2}{3}}$+（$\frac{2}{3}$）-2
=$（\frac{9}{4}）^{\frac{1}{2}}-1-{（\frac{27}{8}）}^{\frac{2}{3}}+{（\frac{3}{2}）}^{2}$
=$\frac{3}{2}-1-（\frac{3}{2}）^{2}+（\frac{3}{2}）^{2}$=$\frac{1}{2}$．…（5分）
（2）（lg2）2+lg2•lg5+$\frac{lo{g}_{3}5}{lo{g}_{3}10}$=lg2（lg2+lg5）+lg5=lg2+lg5=lg10=1．…（10分）
点评 本题考查有理指数幂以及对数运算法则的应用，是基础题．
练习册系列答案
相关题目
18．函数y=$\frac{ln（x-1）}{\sqrt{2-x}}$的定义域为（ ）
| A． | （-∞，2） | B． | （-1，2） | C． | （1，2） | D． | （2，+∞） |
20．下列命题中的真命题是（ ）
| A． | a＞b＞0是1a＜1b的充要条件 | |
| B． | 若a+b+c=0，则a＞b＞c是ac＜0的充分而不必要条件 | |
| C． | ac2＞bc2是a＞b的必要而不充分条件 | |
| D． | a＞b且c＞d是a-c＞b-d的必要不充分条件 |
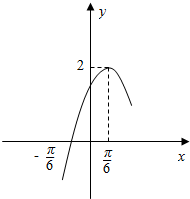函数f（x）=Asin（ωx+φ）（x∈R，A＞0，ω＞0，0＜φ＜$\frac{π}{2}$）的部分图象如图所示．