题目内容
设向量a =(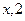 ),b =(
),b =(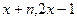 )(
)(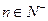 ),函数
),函数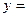 a·b在[0,1]上的最小值与最大值的和为
a·b在[0,1]上的最小值与最大值的和为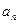 ,又数列{
,又数列{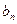 }满足:
}满足: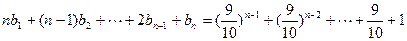 .
.
(1)求证: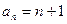 ;
;
(2)求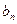 的表达式;
的表达式;
(3)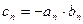 ,试问数列{
,试问数列{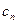 }中,是否存在正整数
}中,是否存在正整数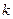 ,使得对于任意的正整数
,使得对于任意的正整数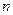 ,都有
,都有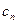 ≤
≤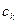 成立?证明你的结论.
成立?证明你的结论.
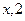 ),b =(
),b =(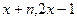 )(
)(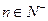 ),函数
),函数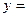 a·b在[0,1]上的最小值与最大值的和为
a·b在[0,1]上的最小值与最大值的和为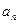 ,又数列{
,又数列{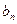 }满足:
}满足: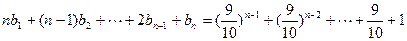 .
.(1)求证:
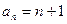 ;
;(2)求
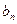 的表达式;
的表达式;(3)
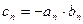 ,试问数列{
,试问数列{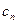 }中,是否存在正整数
}中,是否存在正整数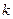 ,使得对于任意的正整数
,使得对于任意的正整数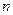 ,都有
,都有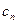 ≤
≤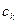 成立?证明你的结论.
成立?证明你的结论.(1)略(2)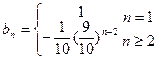 (3)存在正整数
(3)存在正整数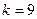 ,使得对于任意的正整数
,使得对于任意的正整数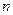 ,都有
,都有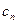 ≤
≤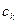 成立.
成立.
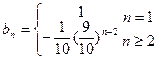 (3)存在正整数
(3)存在正整数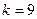 ,使得对于任意的正整数
,使得对于任意的正整数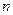 ,都有
,都有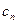 ≤
≤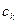 成立.
成立.(1)证明: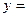 a·b =
a·b =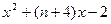 ,因为对称轴
,因为对称轴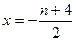 ,
,
所以在[0,1]上为增函数,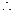
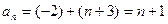 。
。
(2)解:由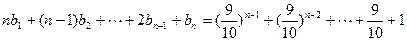
得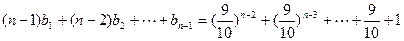
两式相减得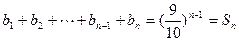 ,
,
当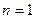 时,
时,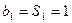
当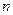 ≥2时,
≥2时,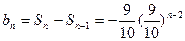
即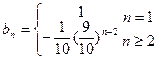
(3)解:由(1)与(2)得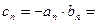
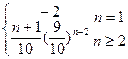
设存在正整数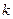 ,使得对于任意的正整数
,使得对于任意的正整数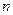 ,都有
,都有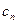 ≤
≤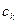 成立,
成立,
当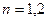 时,
时,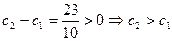
当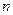 ≥2时,
≥2时,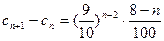 ,
,
所以当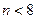 时,
时,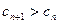 ,
,
当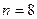 时,
时,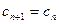 ,
,
当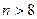 时,
时,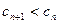
所以存在正整数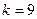 ,使得对于任意的正整数
,使得对于任意的正整数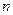 ,都有
,都有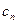 ≤
≤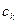 成立.
成立.
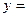 a·b =
a·b =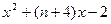 ,因为对称轴
,因为对称轴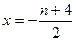 ,
,所以在[0,1]上为增函数,
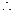
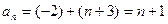 。
。(2)解:由
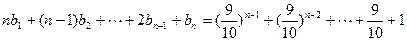
得
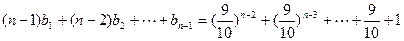
两式相减得
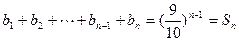 ,
,当
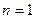 时,
时,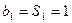
当
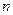 ≥2时,
≥2时,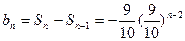
即
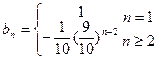
(3)解:由(1)与(2)得
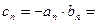
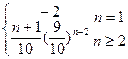
设存在正整数
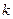 ,使得对于任意的正整数
,使得对于任意的正整数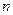 ,都有
,都有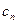 ≤
≤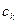 成立,
成立,当
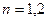 时,
时,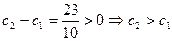
当
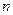 ≥2时,
≥2时,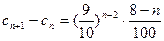 ,
,所以当
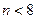 时,
时,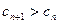 ,
,当
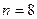 时,
时,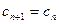 ,
, 当
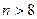 时,
时,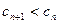
所以存在正整数
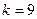 ,使得对于任意的正整数
,使得对于任意的正整数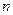 ,都有
,都有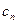 ≤
≤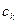 成立.
成立. 
练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
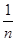 ),f(
),f(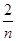 ),
),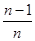 )……,(n≥2,n∈
)……,(n≥2,n∈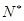 )的前n项的和为Sn ;
)的前n项的和为Sn ;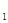 =
=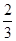 ,a
,a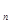 =" "
=" " 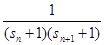 (n≥2,n∈
(n≥2,n∈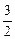 ,a3=f(x).
,a3=f(x).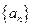 中,
中,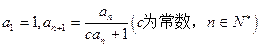 ,且
,且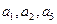 成公比不等于1的等比数列
成公比不等于1的等比数列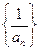 是等差数列; (2)求c的值;
是等差数列; (2)求c的值;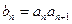 ,数列
,数列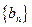 的前
的前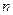 项和为
项和为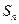 ,求
,求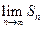
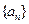 是公方差为
是公方差为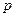 (p>0,an >0)的等方差数列,
(p>0,an >0)的等方差数列,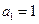 求
求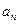 的通项公式;
的通项公式; 已知函数
已知函数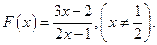
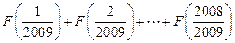 ;(2)已知数列
;(2)已知数列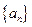 满足
满足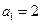 ,
,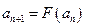 ,求数列
,求数列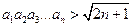 .
.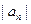 ,
,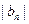 中,a1=2,b1=4,且
中,a1=2,b1=4,且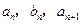 成等差数列,
成等差数列,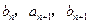 成等比数列(
成等比数列(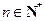 )
)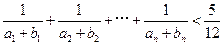 .
.