题目内容
6．函数y=x${\;}^{\frac{2}{3}}$的定义域为[0，+∞），值域为[0，+∞）．分析 直接利用幂函数的性质写出结果即可．
解答 解：函数y=x${\;}^{\frac{2}{3}}$的定义域为：[0，+∞），
函数的值域为：[0，+∞）．
故答案为：[0，+∞）；[0，+∞）．
点评 本题考查幂函数的简单性质的应用，是基础题．
练习册系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
17．
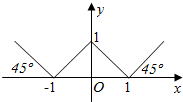函效y=f（x）的图象如图所示，则y=f（x）的解析式是（ ）
函效y=f（x）的图象如图所示，则y=f（x）的解析式是（ ）| A． | f（x）=$\left\{\begin{array}{l}{1-x，x＜1}\\{x-1，x≥1}\end{array}\right.$ | |
| B． | f（x）=$\left\{\begin{array}{l}{-x-1，x＜-1}\\{1+x，-1≤x＜0}\\{1-x，0≤x≤1}\\{x-1，x＞1}\end{array}\right.$ | |
| C． | f（x）=$\left\{\begin{array}{l}{{x}^{2}-1，x＞1或x＜-1}\\{1-{x}^{2}，-1≤x≤1}\end{array}\right.$ | |
| D． | f（x）=$\left\{\begin{array}{l}{{x}^{2}+2x+1，x≤0}\\{{x}^{2}-2x+1，x＞0}\end{array}\right.$ |
