Question

17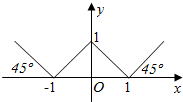．函效y=f（x）的图象如图所示，则y=f（x）的解析式是（　　）

• A． f（x）=$\left\{\begin{array}{l}{1-x，x＜1}\\{x-1，x≥1}\end{array}\right.$
• B． f（x）=$\left\{\begin{array}{l}{-x-1，x＜-1}\\{1+x，-1≤x＜0}\\{1-x，0≤x≤1}\\{x-1，x＞1}\end{array}\right.$
• C． f（x）=$\left\{\begin{array}{l}{{x}^{2}-1，x＞1或x＜-1}\\{1-{x}^{2}，-1≤x≤1}\end{array}\right.$
• D． f（x）=$\left\{\begin{array}{l}{{x}^{2}+2x+1，x≤0}\\{{x}^{2}-2x+1，x＞0}\end{array}\right.$

Answer 1

分析 根据函数的图象结合直线的解析式，代入直线方程求出即可．

解答 解：由图象得：x≤-1时，斜率k=-1，过（-1，0），
故直线的解析式是：y=-x-1，
-1≤x≤0时：直线过（-1，0）（1，0），
故直线的解析式是：y=x+1，
0≤x≤1时：直线过（0，1），（1，0），
故直线的解析式是：y=-x+1，
x≥1时：直线过（1，0），斜率是k=1，
故直线的解析式是：y=x-1，
∴f（x）=$\left\{\begin{array}{l}{-x-1，x＜-1}\\{x+1，-1≤x≤0}\\{-x+1，0＜x＜1}\\{x-1，x≥1}\end{array}\right.$，
故选：B．

点评 本题考查了求函数的解析式问题，考查数形结合，是一道基础题．