题目内容
6.已知函数f(x)是定义在(-∞,0)∪(0,+∞)上的偶函数,当x>0时,f(x)=$\left\{\begin{array}{l}{{2}^{|x-1|}-1,0<x≤2}\\{\frac{1}{2}f(x-2),x>2}\end{array}\right.$,则函数g(x)=4f(x)-1的零点个数为( )| A. | 4 | B. | 6 | C. | 8 | D. | 10 |
分析 令g(x)=0,从而得到f(x)=$\frac{1}{4}$,从而g(x)零点的个数便等于函数f(x)图象和y=$\frac{1}{4}$的图象交点个数,首可以画出f(x)在(0,2]上的图象,而f(x)在(2,+∞)上的图象是将f(x)在(0,2]上的图象向右每次平移2个单位,纵坐标都等于平移前纵坐标的一半.这样即可判断x>6时,f(x)的图象在y=$\frac{1}{4}$图象的下面,并画出f(x)在(0,6]上的图象,根据图象即可判断f(x)在(0,+∞)上的图象和y=$\frac{1}{4}$交点个数,根据偶函数图象的对称性即可得出f(x)在(-∞,0)上的图象和y=$\frac{1}{4}$交点个数,从而最后求出g(x)零点的个数.
解答 解:令g(x)=4f(x)-1=0,则f(x)=$\frac{1}{4}$;断g(x)零点个数,只需判断方程$f(x)=\frac{1}{4}$实数根的个数,即判断函数f(x)和函数y=$\frac{1}{4}$交点个数;
∴需画出f(x)的图象,先来画0<x≤2时,f(x)的图象:
0<x≤2时,f(x)=$\left\{\begin{array}{l}{(\frac{1}{2})^{x-1}-1}&{0<x≤1}\\{{2}^{x-1}-1}&{1<x≤2}\end{array}\right.$,容易画出f(x)在(0,2]上的图象,由f(x)在(2,+∞)上的解析式知道,f(x)在(2,4]上的图象,是f(x)在(0,2]上的图象向右平移2个单位,纵坐标变为原来的$\frac{1}{2}$,这样即可画出f(x)在(0,6]上的图象,而f(x)在x>6时的图象在直线y=$\frac{1}{4}$的下方,所以画出f(x)在(0,6]上的图象如下: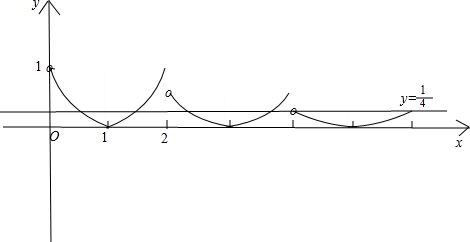
根据图象可看出,在(0,+∞)上,f(x)和y=$\frac{1}{4}$的交点有5个;
∵偶函数的图象关于y轴对称;
∴f(x)在(-∞,0)上的图象和y=$\frac{1}{4}$的图象有5个交点;
∴f(x)的图象和y=$\frac{1}{4}$的图象有10个交点;
∴g(x)零点个数为10.
故选:D.
点评 考查函数零点的概念,偶函数的定义,偶函数图象的对称性,以及方程f(x)=g(x)的解的个数和函数f(x),g(x)交点个数的关系,平移变换以及伸缩变换的概念,指数函数的单调性,含绝对值函数的处理方法:去绝对值.

| A. | f(a+1)>f(2-b) | B. | f(a+1)=f(2-b) | C. | f(a+1)<f(2-b) | D. | 不能确定 |
| API | [0,50] | (50,100] | (100,150] | (150,200] | (200,250] | (250,+∞) |
| 天数 | 6 | 12 | 22 | 30 | 14 | 16 |
(2)API值对部分生产企业有着重大的影响,假设某企业的日利润f(x)与API值x的函数关系为:f(x)=$\left\{\begin{array}{l}40(x≤150)\\ 15(x>150)\end{array}$(单位;万元),利用分层抽样的方式从监测的100天中选出10天,再从这10天中任取3天计算企业利润之和X,求离散型随机变量X的分布列以及数学期望和方差.
| A. | 1006 | B. | 1007 | C. | 1008 | D. | 1009 |
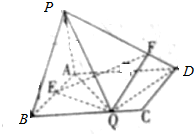 如图所示,在矩形ABCD中,AB=1,AD=a,PA⊥平面ABCD,且PA=1,E为AB中点,F、Q分别在边PD、BC上,$\overrightarrow{PF}$=λ$\overrightarrow{PD}$,λ∈(0,1),且仅存在唯一一点Q,使得PQ⊥QD.
如图所示,在矩形ABCD中,AB=1,AD=a,PA⊥平面ABCD,且PA=1,E为AB中点,F、Q分别在边PD、BC上,$\overrightarrow{PF}$=λ$\overrightarrow{PD}$,λ∈(0,1),且仅存在唯一一点Q,使得PQ⊥QD.