题目内容
13.已知函数f(x)=x2-ax+a-1,a∈R.(1)若f(x)在区间[0,2]上单调,求a的取值范围;
(2)若对于任意a∈(0,4),存在x0∈[0,2],使得t≤|f(x0)|成立,求t的取值范围.
分析 (1)根据二次函数f(x)的图象与性质得,函数的对称轴不在[0,2]内即可;
(2)讨论f(x)在[0,2]上的单调性,求出f(x)在[0,2]的最大、最小值,即可得出t的取值范围.
解答 解:(1)函数f(x)=x2-ax+a-1,a∈R;
当f(x)在区间[0,2]上是单调函数时,
对称轴x=$\frac{a}{2}$应满足$\frac{a}{2}$≤0或$\frac{a}{2}$≥2,
即a≤0或a≥4,
∴a的取值范围是{a|a≤0或a≥4};
(2)∵f(x)=x2-ax+a-1的对称轴为x=$\frac{a}{2}$,
且a∈(0,4),∴$\frac{a}{2}$∈(0,2),
∴函数f(x)=x2-ax+a-1在[0,$\frac{a}{2}$]上是减函数,
在[$\frac{a}{2}$,2]上是增函数;
∴函数f(x)=x2-ax+a-1在[0,2]的最小值为f($\frac{a}{2}$)=-$\frac{{(a-2)}^{2}}{4}$∈(-1,0),
①当$\frac{a}{2}$∈[1,2),即2≤a<4时,
函数f(x)=x2-ax+a-1(x∈[0,2])在x=0时取得最大值,
且最大值为a-1,
由于此时2≤a<4,则1≤a-1<3;
②当$\frac{a}{2}$∈(0,1),即0<a<2时,
函数f(x)=x2-ax+a-1(x∈[0,2])在x=2时取得最大值,
且最大值为22-2a+a-1=3-a,
由于此时0<a<2,则1<3-a<3;
综上,函数f(x)在x∈[0,2]上满足0≤|f(x)|<3,
∴t<3;
即t的取值范围是(-∞,3).
点评 本题考查了二次函数的图象与性质的应用问题,也考查了恒成立问题与存在性问题,是综合性题目.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
3.若0<a<1,0<b<1且a≠b,则a+b、2$\sqrt{ab}$、2ab、a2+b2中最大的一个是( )
| A. | a+b | B. | 2$\sqrt{ab}$ | C. | 2ab | D. | a2+b2 |
5.在△ABC中,AB=3,BC=$\sqrt{13}$,AC=4,则AC边上的高等于( )
| A. | $\frac{3}{2}$$\sqrt{3}$ | B. | $\frac{3}{2}$$\sqrt{2}$ | C. | 3 | D. | 3$\sqrt{3}$ |
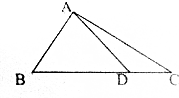 已知在△ABC中,点D在BC上,且满足$\overrightarrow{BD}$=3$\overrightarrow{DC}$,若$\overrightarrow{AD}$=x$\overrightarrow{AB}$+y$\overrightarrow{AC}$,则x+y=1.
已知在△ABC中,点D在BC上,且满足$\overrightarrow{BD}$=3$\overrightarrow{DC}$,若$\overrightarrow{AD}$=x$\overrightarrow{AB}$+y$\overrightarrow{AC}$,则x+y=1.