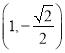Question

【题目】已知A，B分别是直线y=x和y=﹣x上的两个动点，线段AB的长为2 ，D是AB的中点．
（1）求动点D的轨迹C的方程；
（2）若过点（1，0）的直线l与曲线C交于不同两点P、Q，
①当|PQ|=3时，求直线l的方程；
②试问在x轴上是否存在点E（m，0），使 恒为定值？若存在，求出E点的坐标及定值；若不存在，请说明理由．

Answer 1

【答案】
（1）解：设D（x，y），A（a，a），B（b，﹣b），

∵D是AB的中点，∴x= ，y= ，

∵|AB|=2 ，∴（a﹣b）2+（a+b）2=12，

∴（2y）2+（2x）2=12，∴点D的轨迹C的方程为x2+y2=3

（2）解：①当直线l与x轴垂直时，P（1， ），Q（1，﹣ ），此时|PQ|=2 ，不符合题意；

当直线l与x轴不垂直时，设直线l的方程为y=k（x﹣1），由于|PQ|=3，所以圆心C到直线l的距离为 ，

由 = ，解得k=± ．故直线l的方程为y=± （x﹣1）．

②当直线l的斜率存在时，设其斜率为k，则l的方程为y=k（x﹣1），

由消去y得（k2+1）x2﹣2k2x+k2﹣3=0，

设P（x1，y1），Q（x2，y2）则由韦达定理得x1+x2= ，x1x2= ，

则 =（m﹣x1，﹣y1）， =（m﹣x2，﹣y2），

∴ =（m﹣x1）（m﹣x2）+y1y2=m2﹣m（x1+x2）+x1x2+y1y2

=m2﹣m（x1+x2）+x1x2+k2（x1﹣1）（x2﹣1）

=m2﹣ + +k2 （ ﹣ +1）=

要使上式为定值须 =1，解得m=1，∴ 为定值﹣2，

当直线l的斜率不存在时P（1， ），Q（1，﹣ ），

由E（1，0）可得 =（0，﹣ ）， =（0， ），

∴ =﹣2，

综上所述当E（1，0）时， 为定值﹣2

【解析】（1）设D（x，y），A（a，a），B（b，﹣b），然后根据线段AB的长为2 ，D是AB的中点消去a与b，得到x与y的等量关系，即为动点D的轨迹C的方程；（2）①讨论直线l与x轴是否垂直，然后利用点到直线的距离公式建立等式关系，从而求出直线方程；②讨论直线l的斜率是否存在，不存在时直接求 ，存在时，将直线与圆联立方程组，消去y，然后设P（x1 ， y1），Q（x2 ， y2），将 表示出来，使其与k无关即可求出m的值．