题目内容
16.在△ABC中,a,b,c分别为内角A,B,C的对边,已知b=6,且(2c-a)cosB=bcosA,若△ABC的两条中线AE、CF相交于点D,则四边形BEDF的面积的最大值为3$\sqrt{3}$.分析 利用正弦定理化简已知条件,根据三角形的内角和定理及诱导公式化简,由sinC不为0,得到cosB的值,由B的范围,利用特殊角的三角函数值即可得到B的度数,由余弦定理及基本不等式可求S△ABC的最大值,求出EF=$\frac{1}{2}$AC,EF∥AC,证相似求出△BEF的面积,求出△ACE的面积,求出△ADC的面积,根据相似求出△DEF的面积,相加即可得出答案.
解答 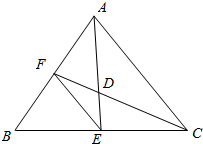 解:由已知及正弦定理得:(2sinC-sinA)cosB-sinBcosA=0,
解:由已知及正弦定理得:(2sinC-sinA)cosB-sinBcosA=0,
即2sinCcosB-sin(A+B)=0,
在△ABC中,由sin(A+B)=sinC
故sinC(2cosB-1)=0,
由B,C∈(0,π),则2cosB-1=0,
所以B=60°;
所以由余弦定理可得:36=AB2+BC2-AB•BC≥2AB•BC-AB•BC=AB•BC,
所以S△ABC=$\frac{1}{2}$AB•BC•sin60°≤9$\sqrt{3}$,
连接FE,
∵△ABC的中线为AE,CF,
∴FE=$\frac{1}{2}$AC,FE∥AC,
∴△BEF∽△CBA,
∵△ABC的面积的最大值为9$\sqrt{3}$,
∴$\frac{9\sqrt{3}}{{S}_{△BEF}}$=4,
∴S△BEF的最大值为$\frac{9\sqrt{3}}{4}$,
∵△DEF∽△ADC,
∴$\frac{EF}{AC}=\frac{DE}{AD}=\frac{FD}{DC}=\frac{1}{2}$,
∵△ABC的面积最大值为9$\sqrt{3}$,AE为△ABC的中线,
∴△ACE的面积为$\frac{1}{2}$×9$\sqrt{3}$=$\frac{9\sqrt{3}}{2}$,
∴△ADC的面积为:$\frac{2}{3}×$$\frac{9\sqrt{3}}{2}$=3$\sqrt{3}$,
∵△DEF∽△ADC,
∴△DEF的面积S=$\frac{1}{4}$×3$\sqrt{3}$=$\frac{3\sqrt{3}}{4}$,
∴四边形DCEF的面积是$\frac{9\sqrt{3}}{4}$+$\frac{3\sqrt{3}}{4}$=3$\sqrt{3}$.
故答案为:3$\sqrt{3}$.
点评 此题考查学生灵活运用正弦定理及诱导公式化简求值,灵活运用三角形的面积公式及两角和的正弦函数公式化简求值,掌握正弦函数的值域,考查三角形的中位线定理,三角形的面积,相似三角形的性质和判定的应用,解此题的关键是求出各个三角形的面积,属于中档题.

 一本好题口算题卡系列答案
一本好题口算题卡系列答案| A. | 等边三角形 | B. | 等腰三角形 | C. | 等腰直角三角形 | D. | 直角三角形 |
| A. | 1,$\frac{1}{2}$ | B. | $\frac{1}{2}$,1 | C. | $\frac{1}{2}$,$\frac{1}{4}$ | D. | $\frac{1}{4}$,$\frac{1}{2}$ |
| A. | [1,2) | B. | [$\frac{4}{3}$,2] | C. | ($\frac{4}{3}$,2) | D. | [$\frac{4}{3}$,2) |
