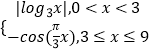题目内容
【题目】已知O为坐标原点，设动点M（2，t）（t＞0）．
（1）若过点P（0，4 
）的直线l与圆C：x2+y2﹣8x=0相切，求直线l的方程；
（2）求以OM为直径且被直线3x﹣4y﹣5=0截得的弦长为2的圆的方程；
（3）设A（1，0），过点A作OM的垂线与以OM为直径的圆交于点N，求证：线段ON的长为定值，并求出这个定值．
【答案】
（1）解：圆C：x2+y2﹣8x=0化为（x﹣4）2+y2=16，得到圆心C（4，0），半径r=4．
斜率不存在时，x=0满足题意；
斜率存在时，设切线方程为y=kx+4 
，即kx﹣y+4 =0，
根据圆心到切线的距离等于半径可得4= 
，解得k=﹣ 
，
故切线方程为y=﹣ x+4 ，
综上所述，直线l的方程为y=﹣ x+4 或x=0
（2）解：以OM为直径的圆的方程为（x﹣1）2+（y﹣ 
）= 
+1，
其圆心为（1， ），半径r= 
因为以OM为直径的圆被直线3x﹣4y﹣5=0截得的弦长为2
所以圆心到直线3x﹣4y﹣5=0的距离d= 
= ，解得t=4
所求圆的方程为（x﹣1）2+（y﹣2）2=5
（3）证明：设N（x0，y0），则 
=（x0﹣1，y0）， 
=（2，t）， 
=（x0﹣2，y0﹣t）， 
=（x0，y0），
∵ ⊥ ，∴2（x0﹣1）+ty0=0，∴2x0+ty0=2，
又∵ ⊥ ，∴x0（x0﹣2）+y0（y0﹣t）=0，
∴x02+y02=2x0+ty0=2，
所以| |= 
= 
为定值
【解析】（1）圆C：x2+y2﹣8x=0化为（x﹣4）2+y2=16，得到圆心C（4，0），半径r=4，分类讨论即可求直线l的方程；（2）设出以OM为直径的圆的方程，变为标准方程后找出圆心坐标和圆的半径，由以OM为直径的圆被直线3x﹣4y﹣5=0截得的弦长，过圆心作弦的垂线，根据垂径定理得到垂足为中点，由弦的一半，半径以及圆心到直线的距离即弦心距构成直角三角形，利用点到直线的距离公式表示出圆心到3x﹣4y﹣5=0的距离d，根据勾股定理列出关于t的方程，求出方程的解即可得到t的值，即可确定出所求圆的方程；（3）设出点N的坐标，由 ⊥ 得到两向量的数量积为0，利用平面向量的数量积的运算法则表示出一个关系式，又 ⊥ ，同理根据平面向量的数量积的运算法则得到另一个关系式，把前面得到的关系式代入即可求出线段ON的长，从而得到线段ON的长为定值．
