题目内容
【题目】已知关于![]() 的函数
的函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)设![]() ,讨论函数
,讨论函数![]() 的单调区间;
的单调区间;
(3)若函数![]() 没有零点,求实数
没有零点,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)见解析;(3)
;(2)见解析;(3)![]()
【解析】试题分析:(1)当![]() 时,得到函数解析式
时,得到函数解析式![]() ,求得
,求得![]() ,得到
,得到![]() ,得出切线的斜率,再利用点斜式求解直线的方程;
,得出切线的斜率,再利用点斜式求解直线的方程;
(2)由题意,求出![]() 的解析式,求得
的解析式,求得![]() ,可分
,可分![]() 和
和![]() 两种情况分类讨论,即可求解函数的单调区间;
两种情况分类讨论,即可求解函数的单调区间;
(3)由![]() 没有零点,转化为方程
没有零点,转化为方程![]() 无解,即
无解,即![]() 与
与![]() 两图象无交点,列出条件,即可求解实数的取值范围.
两图象无交点,列出条件,即可求解实数的取值范围.
试题解析:
(1)当![]() 时,
时, ![]() ,
, 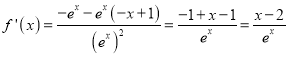 ,
,
![]() ,∴
,∴![]() ,即
,即![]() 在
在![]() 处的切线方程为
处的切线方程为![]() .
.
(2)∵ ,
, ![]() ,当
,当![]() 时,
时,
![]() 在
在![]() 上恒成立,∴
上恒成立,∴![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,令
时,令![]() ,解得
,解得![]() ,
,
令![]() ,解得
,解得![]() ,∴
,∴![]() 在
在![]() 单调递增,在
单调递增,在![]() 单调递减.
单调递减.
(3)∵![]() 没有零点,
没有零点,
即![]() 无解,∴
无解,∴![]() 与
与![]() 两图象无交点,
两图象无交点,
设两图象相切于![]() 两点,∴
两点,∴![]() ,∴
,∴![]() ,
, ![]() ,∵两图象无交点,∴
,∵两图象无交点,∴![]() .
.

练习册系列答案
相关题目