题目内容
3.已知函数$f(x)=sin(2x+\frac{π}{3})+sin(2x-\frac{π}{3})+a{cos^2}$x+b,x∈R,且$f(0)=f(\frac{π}{4})=1$.(Ⅰ)求a,b的值及f(x)的最小正周期;
(Ⅱ)求函数f(x)在区间$[-\frac{π}{4}{,_{\;}}\frac{π}{4}]$上的最大值和最小值.
分析 (Ⅰ)首先利用函数f(0)=f($\frac{π}{4}$)=1,建立方程组求出a和b的值,进一步听过三角函数的恒等变换求出函数的正弦形式,进一步求出函数的最小正周期.
(Ⅱ)直接利用函数的关系式,利用函数的定义域求出函数的值域,最后求出函数的最值.
解答 解:(Ⅰ)$f(x)=sin(2x+\frac{π}{3})+sin(2x-\frac{π}{3})+aco{s}^{2}$x+b
由于:f(0)=f($\frac{π}{4}$)=1,
所以:$\left\{\begin{array}{l}\frac{\sqrt{3}}{2}-\frac{\sqrt{3}}{2}+a+b=1\\ \frac{1}{2}+\frac{1}{2}+\frac{1}{2}a+b=1\end{array}\right.$,
解得:$\left\{\begin{array}{l}a=2\\ b=-1\end{array}\right.$
所以:$f(x)=sin(2x+\frac{π}{3})+sin(2x-\frac{π}{3})+$2cos2x-1
=sin2x+cos2x
=$\sqrt{2}sin(2x+\frac{π}{4})$,
所以:函数的最小正周期:T=$\frac{2π}{2}=π$,
(Ⅱ)由于:函数f(x)=$\sqrt{2}sin(2x+\frac{π}{4})$,
当$-\frac{π}{4}≤x≤\frac{π}{4}$时,$-\frac{π}{4}≤2x+\frac{π}{4}≤\frac{3π}{4}$.
所以:$-1≤\sqrt{2}sin(2x+\frac{π}{4})≤\sqrt{2}$
即:函数的最大值为$\sqrt{2}$,函数的最小值为-1.
点评 本题考查的知识要点:利用待定系数法求函数的解析式,三角函数的恒等变换,正弦型函数的周期的确定,利用函数的定义域求函数的值域,主要考查学生的应用能力.

| A. | -2 | B. | 2 | C. | -1 | D. | $\frac{1}{2}$ |
| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | 4 |
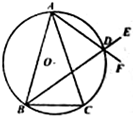 已知△ABC中,AB=AC,D是△ABC外接圆上$\widehat{AC}$上的点(不与点A、C重合),延长BD至F.
已知△ABC中,AB=AC,D是△ABC外接圆上$\widehat{AC}$上的点(不与点A、C重合),延长BD至F.