题目内容
14. 已知△ABC中,AB=AC,D是△ABC外接圆上$\widehat{AC}$上的点(不与点A、C重合),延长BD至F.
已知△ABC中,AB=AC,D是△ABC外接圆上$\widehat{AC}$上的点(不与点A、C重合),延长BD至F.(1)求证:AD延长线DF平分∠CDE;
(2)若∠BAC=30°,△ABC中BC边上的高为2+$\sqrt{3}$,求△ABC外接圆的面积.
分析 (1)根据A,B,C,D四点共圆,可得∠ABC=∠CDF,AB=AC可得∠ABC=∠ACB,从而得解.
(2)设O为外接圆圆心,连接AO并延长交BC于H,则AH⊥BC.连接OC,设圆半径为r,则r+$\frac{\sqrt{3}}{2}$r=2+$\sqrt{3}$,求出r,即可求△ABC外接圆的面积.
解答 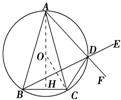 (1)证明:如图,∵A,B,C,D四点共圆,∴∠CDF=∠ABC.
(1)证明:如图,∵A,B,C,D四点共圆,∴∠CDF=∠ABC.
又AB=AC,∴∠ABC=∠ACB,
且∠ADB=∠ACB,∴∠ADB=∠CDF,
又由对顶角相等得∠EDF=∠ADB,故∠EDF=∠CDF,
即AD的延长线DF平分∠CDE.…(5分)
(2)解:设O为外接圆圆心,连接AO并延长交BC于H,则AH⊥BC.连接OC,
由题意∠OAC=∠OCA=15°,∠ACB=75°,∴∠OCH=60°,
设圆半径为r,则r+$\frac{\sqrt{3}}{2}$r=2+$\sqrt{3}$,得r=2,外接圆的面积为4π.…(10分)
点评 本题以圆为载体,考查圆的内接四边形的性质,考查等腰三角形的性质,考查外接圆的面积,属于中档题.

练习册系列答案
相关题目
4.“x2-4x-5=0”是“x=5”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |