题目内容
5.已知数列{an}、{bn},数列{an}的前n项和为Sn,且对任意自然数n,总有Sn=p(an-1),(p是常数且p≠0,p≠1).数列{bn}中,bn=2n+q(q是常数),且a1=b1,a2<b2,求:(1)求数列{an}的通项公式.
(2)求p的取值范围.
分析 (1)通过令n=1易知${a_1}=\frac{p}{p-1}$,当n≥2时利用an=Sn-Sn-1可知数列{an}是首项、公比均为$\frac{p}{p-1}$的等比数列,进而计算可得结论;
(2)通过(1)及a1=b1、a2<b2,联立二式并消去q整理、计算可知p<$\frac{1}{2}$或p>2,进而可得结论.
解答 解:(1)依题意,a1=S1=p(a1-1),即${a_1}=\frac{p}{p-1}$,
n≥2时,an=Sn-Sn-1=p(an-an-1),
∴(p-1)an=pan-1,
∴数列{an}是首项、公比均为$\frac{p}{p-1}$的等比数列,
∴$a_n^{\;}=\frac{p}{p-1}•{(\frac{p}{p-1})^{n-1}}={(\frac{p}{p-1})^n}$;
(2)依题意,$\frac{p}{p-1}=2+q,{(\frac{p}{p-1})^2}<4+q$,
消去q并整理得:${(\frac{p}{p-1})^2}-\frac{p}{p-1}-2<0$,
解得:$-1<\frac{p}{p-1}<2$,
∴p<$\frac{1}{2}$或p>2,
∴p的取值范围是:(-∞,0)∪(0,$\frac{1}{2}$)∪(2,+∞).
点评 本题考查数列的通项,注意解题方法的积累,属于中档题.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
3.已知log89=a,log25=b,则lg3=( )
| A. | $\frac{a}{b-1}$ | B. | $\frac{3}{2(b-1)}$ | C. | $\frac{3a}{2(b+1)}$ | D. | $\frac{3(a-1)}{2b}$ |
13.甲、乙两车从A地沿同一路线到达B地,甲车一半时间的速度为a,另一半时间的速度为b,乙车用速度a行走了一半路程,用速度b行走了另一半路程,若a≠b,则两车到达B地的情况是( )
| A. | 甲车先到达B地 | B. | 甲车先到达B地 | C. | 同时到达 | D. | 不能判断 |
14.把-1125°化成α+2kπ(0≤α<2π,k∈Z=)的形式是( )
| A. | -$\frac{π}{4}$-6π | B. | $\frac{7π}{4}$-6π | C. | -$\frac{π}{4}$-8π | D. | $\frac{7π}{4}$-8π |
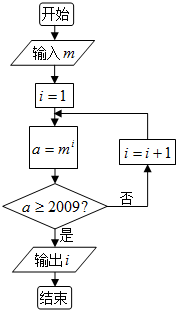 阅读框图,若输入m=3,则输出i=7.(参考数值:log32009≈6.923)
阅读框图,若输入m=3,则输出i=7.(参考数值:log32009≈6.923)