题目内容
【题目】已知A={x|x2≥9},B={x|﹣1<x≤7},C={x||x﹣2|<4}.
(1)求A∩B及A∪C;
(2)若U=R,求![]() .
.
【答案】(1) A∩B={x|3≤x≤7},A∪C={x|x≤﹣3或x>﹣2} (2) A∩U(B∩C)={x|x≥6或x≤﹣3}
【解析】试题分析:首先解不等式,化简集合A和C,再利用集合运算求出集合A与B的交集及集合A与C的并集;再求出集合B与C的交集,再求出B和C交集的补集,最后再求与集合A的交集.解题时注意集合的交、并、补的运算的定义,无限数集求交、并、补时,使用的工具是数轴.
试题解析:
(1)集合A中的不等式解得:x≥3或x≤﹣3,即A={x|x≥3或x≤﹣3};
集合C中的不等式解得:﹣2<x<6,即C={x|﹣2<x<6},
∴A∩B={x|3≤x≤7},A∪C={x|x≤﹣3或x>﹣2};
(2)∵B∩C={x|﹣1<x<6},全集U=R,
∴U(B∩C)={x|x≤﹣1或x≥6},
则A∩U(B∩C)={x|x≥6或x≤﹣3}

 优学名师名题系列答案
优学名师名题系列答案【题目】随着电子商务的发展,人们的购物习惯正在改变,基本上所有的需求都可以通过网络购物解决.小王是位网购达人,每次购买商品成功后都会对电商的商品和服务进行评价.现对其近年的200次成功交易进行评价统计,统计结果如下表所示.
对服务好评 | 对服务不满意 | 合计 | |
对商品好评 | 80 | 40 | 120 |
对商品不满意 | 70 | 10 | 80 |
合计 | 150 | 50 | 200 |
(1)是否有![]() 的把握认为商品好评与服务好评有关? 请说明理由;
的把握认为商品好评与服务好评有关? 请说明理由;
(2)现从这200次交易中,按照“对商品好评”和“对商品不满意”采用分层抽样取出5次交易,然后从这5次交易中任选两次进行观察,求这两次交易中恰有一次“对商品好评”的概率.
附: (其中
(其中![]() )
)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
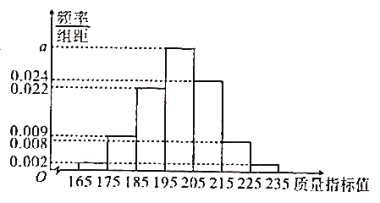
【题目】为迎接2022年北京冬季奥运会,普及冬奥知识,某校开展了“冰雪答题王”冬奥知识竞赛活动.现从参加冬奥知识竞赛活动的学生中随机抽取了100名学生,将他们的比赛成绩(满分为100分)分为6组:![]() ,
,![]() 得到如图所示的频率分布直方图.
得到如图所示的频率分布直方图.
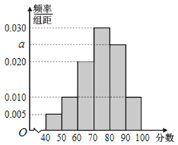
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)记![]() 表示事件“从参加冬奥知识竞赛活动的学生中随机抽取一名学生,该学生的比赛成绩不低于80分”,估计
表示事件“从参加冬奥知识竞赛活动的学生中随机抽取一名学生,该学生的比赛成绩不低于80分”,估计![]() 的概率;
的概率;
(Ⅲ)在抽取的100名学生中,规定:比赛成绩不低于80分为“优秀”,比赛成绩低于80分为“非优秀”.请在答题卡上将![]() 列联表补充完整,并判断是否有
列联表补充完整,并判断是否有![]() 的把握认为“比赛成绩是否优秀与性别有关”?
的把握认为“比赛成绩是否优秀与性别有关”?
参考公式及数据: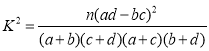 ,
,![]() .
.
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |