题目内容
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD为直角梯形,BC∥AD,AB⊥BC,∠ADC=45°,PA⊥平面ABCD,AB=AP=1,AD=3.
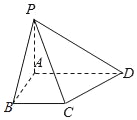
(1)求异面直线PB与CD所成角的大小;
(2)求点D到平面PBC的距离.
【答案】(1)![]() ; (2)见解析.
; (2)见解析.
【解析】
(1)建立空间直角坐标系,利用向量法求异面直线PB与CD所成角大小.
(2)求出平面PBC的一个法向量,利用向量法的距离公式求点D到平面PBC的距离.
(1)以A为原点,AB为x轴,AD为y轴,AP为z轴,建立如图所示空间直角坐标系,
则P(0,0,1),B(1,0,0),C(1,2,0)D(0,3,0),
∴![]() =(1,0,﹣1),
=(1,0,﹣1),![]() =(﹣1,1,0),
=(﹣1,1,0),
设异面直线PB与CD所成角为θ,
则cosθ=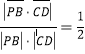 ,
,
所以异面直线PB与CD所成角大小为![]() .
.
(2)设平面PBC的一个法向量为![]() =(x,y,z),
=(x,y,z),
![]() =(1,0,﹣1),
=(1,0,﹣1),![]() =(0,2,0),
=(0,2,0),![]() =(﹣1,1,0),
=(﹣1,1,0),
则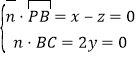 ,取x=1,得
,取x=1,得![]() =(1,0,1),
=(1,0,1),
∴点D到平面PBC的距离d=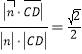 .
.

练习册系列答案
相关题目
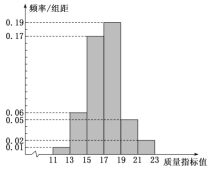
【题目】从甲地到乙地沿某条公路行驶一共200公里,遇到红灯个数的概率如下表所示:
红灯个数 | 0 | 1 | 2 | 3 | 4 | 5 | 6个及6个以上 |
概率 | 0.02 | 0.1 |
| 0.35 | 0.2 | 0.1 | 0.03 |
(1)求表中字母![]() 的值;
的值;
(2)求至少遇到4个红灯的概率;
(3)求至多遇到5个红灯的概率.