题目内容
【题目】设椭圆M:![]()
![]() 的离心率与双曲线
的离心率与双曲线![]() 的离心率互为倒数,且内切于圆
的离心率互为倒数,且内切于圆![]() 。
。
(1)求椭圆M的方程;
(2)已知![]() ,
,![]() 是椭圆M的下焦点,在椭圆M上是否存在点P,使
是椭圆M的下焦点,在椭圆M上是否存在点P,使![]() 的周长最大?若存在,请求出
的周长最大?若存在,请求出![]() 周长的最大值,并求此时
周长的最大值,并求此时![]() 的面积;若不存在,请说明理由。
的面积;若不存在,请说明理由。
【答案】(1)![]() ; (2)
; (2)![]() .
.
【解析】
(1)双曲线的离心率为![]() ,∴椭圆的离心率为
,∴椭圆的离心率为![]()
∵椭圆M内切于圆![]()
![]() 得解。
得解。
(2)椭圆的焦点为![]() ,由椭圆的定义得:
,由椭圆的定义得:![]()
![]() 的周长为
的周长为![]()
当且仅当点P在线段![]() 的延长线上时取等号。
的延长线上时取等号。
∴在椭圆M上存在点P,使![]() 的周长取得最大值
的周长取得最大值![]() ,
,
直线![]() 的方程为
的方程为![]() ,由 ∵点P在线段
,由 ∵点P在线段![]() 的延长线上,∴点P的坐标为
的延长线上,∴点P的坐标为![]() ,再求解
,再求解![]() 的面积。
的面积。
(1)∵双曲线![]() 的离心率为
的离心率为![]() ,∴椭圆M的离心率为
,∴椭圆M的离心率为![]()
∵椭圆M内切于圆![]()
![]()
得: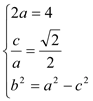
![]()
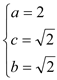 所求椭圆M的方程为
所求椭圆M的方程为![]() .
.
(2)椭圆M的上焦点为![]() ,由椭圆的定义得:
,由椭圆的定义得:![]()
![]() 的周长为
的周长为![]()
当且仅当点P在线段![]() 的延长线上时取等号。
的延长线上时取等号。
∴在椭圆M上存在点P,使![]() 的周长取得最大值
的周长取得最大值![]() ,
,
直线![]() 的方程为
的方程为![]() ,由
,由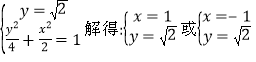
∵点P在线段![]() 的延长线上,∴点P的坐标为
的延长线上,∴点P的坐标为![]() ,
,
![]() 的面积
的面积![]() 。
。

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目