Question

【题目】试证明：集合满足

（1）对每个及，若，则一定不是的倍数；

（2）对每个（表示在中的补集），且，必存在，，使是的倍数.

Answer 1

【答案】（1）见解析（2）见解析

【解析】

（1）对任意，设.则.

若是任意一个小于的正整数，则.

由于与中，一个为奇数，它不含质因子2，另一个为偶数，它含质因子2的幂的次数最多为，因此，一定不是的倍数.

（2）若，且，设，其中，，为大于1的奇数.

则.

下面给出三种证明方法.

方法1 令，.

消去得.

由，知方程必有整数解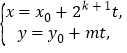

其中，，为方程的特解.

记最小的正整数解为.则.

故，使得是的倍数.

方法2 注意到，，由中国剩余定理，知同余方程组

在区间上有解，即存在，使得是的倍数.

方法3 由，总存在，使得.

取，使得.则.

存在，使得.

此时，.

从而是的倍数.