题目内容
【题目】设f(x)="xln" x–ax2+(2a–1)x，a
R.
（Ⅰ）令g(x)=f'(x)，求g(x)的单调区间；
（Ⅱ）已知f(x)在x=1处取得极大值.求实数a的取值范围.
【答案】（Ⅰ）当
时，函数
单调递增区间为
，当
时，函数
单调递增区间为
，单调递减区间为
； （Ⅱ）
【解析】试题分析：（Ⅰ）先求出
，然后讨论当
时，当
时的两种情况即得.
（Ⅱ）分以下情况讨论：①当
时，②当
时，③当
时，④当
时，综合即得.
试题解析：（Ⅰ）由
可得
，
则
，
当
时，
时， 
，函数
单调递增；
当
时，
时， 
，函数
单调递增，
时， 
，函数
单调递减.
所以当
时， 
单调递增区间为
；
当
时，函数
单调递增区间为
，单调递减区间为
.
（Ⅱ）由（Ⅰ）知， 
.
①当
时， 
， 
单调递减.
所以当
时， 
， 
单调递减.
当
时， 
， 
单调递增.
所以
在x=1处取得极小值，不合题意.
②当
时， 
，由(Ⅰ)知
在
内单调递增，
可得当当
时， 
， 
时， 
，
所以
在(0,1)内单调递减，在
内单调递增，
所以
在x=1处取得极小值，不合题意.
③当
时，即
时， 
在(0,1)内单调递增，在
内单调递减，
所以当
时， 
， 
单调递减，不合题意.
④当
时，即
，当
时， 
， 
单调递增,
当
时， 
， 
单调递减，
所以f(x)在x=1处取得极大值，合题意.
综上可知，实数a的取值范围为
.
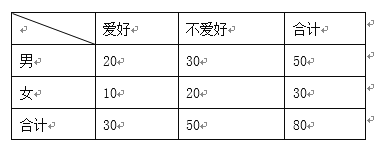
【题目】为了政府对过热的房地产市场进行调控决策，统计部门对城市人和农村人进行了买房心理预测调研，用简单随机抽样的方法抽取了110人进行统计，得到如下列联表：
买房 | 不买房 | 纠结 | |
城市人 | 5 | 15 | |
农村人 | 20 | 10 |
已知样本中城市人数与农村人数之比是3：8．
（Ⅰ）分别求样本中城市人中的不买房人数和农村人中的纠结人数；
（Ⅱ）从参与调研的城市人中用分层抽样方法抽取6人，进一步统计城市人的某项收入指标，假设一个买房人的指标算作3，一个纠结人的指标算作2，一个不买房人的指标算作1，现在从这6人中再随机选取3人，令X=再抽取3人指标之和，求X的分布列和数学期望．