题目内容
1.设函数f(x)的定义域为D,若函数f(x)满足条件:存在[a,b]⊆D,使得f(x)在区间[a,b]上的值域为[$\frac{a}{n},\frac{b}{n}$](n∈N*),则称g(x)为“n倍缩函数”,若函数f(x)=log3(3x+t)为“3倍缩函数”,则t的取值范围为( )| A. | (0,$\frac{1}{3}$) | B. | (0,$\frac{2\sqrt{3}}{9}$) | C. | (0,$\frac{\sqrt{3}}{3}$) | D. | (0,1) |
分析 问题转化为t=${3}^{\frac{x}{3}}$-3x有两个不同的解,令${3}^{\frac{x}{3}}$=m,换元可得t=m-m3有两个不同的正数解,即y=t与y=m-m3有两个不同交点,求导数可得y=m-m3在(0,$\frac{\sqrt{3}}{3}$)上单调递增,在($\frac{\sqrt{3}}{3}$,+∞)单调递减,可得y取最大值,可得t的范围.
解答 解:由题意可得[a,b]⊆D,使得log3(3a+t)=$\frac{a}{3}$,log3(3b+t)=$\frac{b}{3}$,
即方程log3(3x+t)=$\frac{x}{3}$有两个不同的解,即3x+t=${3}^{\frac{x}{3}}$有两个不同的解,
变形可得t=${3}^{\frac{x}{3}}$-3x有两个不同的解,令${3}^{\frac{x}{3}}$=m,则m>0
换元可得t=m-m3有两个不同的正数解,
即y=t与y=m-m3有两个不同交点,
求导数可得y′=1-3m2,
由y′=1-3m2<0可解得m<-$\frac{\sqrt{3}}{3}$或m>$\frac{\sqrt{3}}{3}$,
∴y=m-m3在(0,$\frac{\sqrt{3}}{3}$)上单调递增,在($\frac{\sqrt{3}}{3}$,+∞)单调递减,
当m=$\frac{\sqrt{3}}{3}$时,y取最大值$\frac{2\sqrt{3}}{9}$,
∴要使y=t与y=m-m3有两个不同交点需0<t<$\frac{2\sqrt{3}}{9}$,
故选:B.
点评 本题考查函数的值域,涉及导数法判函数的单调性和转化的思想以及新定义,属中档题

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.函数f(x)=x3-3x-1,x∈[-3,2].则f(x)的最大值与最小值的差为( )
| A. | 20 | B. | 18 | C. | 4 | D. | 0 |
13.已知M(3,-2),N(-5,-1),若$\overrightarrow{MP}=\frac{1}{2}\overrightarrow{MN}$,则P点的坐标为( )
| A. | (-8,1) | B. | (8,-1) | C. | $(-1,-\frac{3}{2})$ | D. | $(1,\frac{3}{2})$ |
10.等差数列{an},{bn}的前n项和分别为Sn,Tn,若$\frac{{S}_{n}}{{T}_{n}}$=$\frac{2n+4}{3n+1}$,则an=bn时n=( )
| A. | 2 | B. | 6 | C. | 无解 | D. | 无数多个 |
11.设函数f(x)=$\frac{1}{3}$x3-2f′(0)ex+3x-1,则f(0)=( )
| A. | -3 | B. | 3 | C. | -1 | D. | 5 |
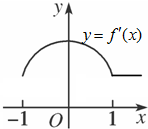 已知函数y=f(x)的图象是下列四个图象之一,且其导函数y=f′(x)的图象如图所示,则该函数的图象可能是( )
已知函数y=f(x)的图象是下列四个图象之一,且其导函数y=f′(x)的图象如图所示,则该函数的图象可能是( )