��Ŀ����
����Ŀ��һ�����д�С��ͬ��4�������2�����������н��ۣ�
�ٴ�����ȡ3��ǡ��һ������ĸ�����![]() ��
��
�ڴ����зŻص�ȡ��6�Σ�ÿ����ȡһ����ȡ����������ķ���Ϊ![]() ��
��
���ִ��в��Żص�ȡ��2�Σ�ÿ����ȡ1�����ڵ�һ��ȡ������������£��ڶ����ٴ�ȡ������ĸ���Ϊ![]() ��
��
�ܴ����зŻص�ȡ��3�Σ�ÿ����ȡһ����������һ��ȡ������ĸ���Ϊ![]() .
.
����������ȷ���۵������________��
���𰸡��٢ڢ�.
��������
�����ݹŵ�����ʹ�ʽ������֪ʶ�ɵý����������ݶ���ֲ��ķ��ʽ�ɵý����
�������������ʽ��м���ɵõ��ڶ����ٴ�ȡ������ĸ����������ݶ����¼��ĸ��ʹ�ʽ�ɵý��.
�ٴ�����ȡ3����ǡ��һ������ĸ�����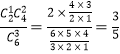 ���ʢ���ȷ��
���ʢ���ȷ��
�������зŻص�ȡ��![]() �Σ�ÿ����ȡһ��
�Σ�ÿ����ȡһ��
ȡ���������![]() ���䷽��Ϊ
���䷽��Ϊ![]() ���ʢ���ȷ��
���ʢ���ȷ��
�����в��Żص�ȡ��![]() ����ÿ����ȡһ�����ڵ�һ��ȡ�������ʱ���л���
����ÿ����ȡһ�����ڵ�һ��ȡ�������ʱ���л���![]() ������
������![]() ��������ڶ����ٴ�ȡ������ĸ���Ϊ
��������ڶ����ٴ�ȡ������ĸ���Ϊ![]() ���ʢ۴���
���ʢ۴���
�������зŻص�ȡ��3����ÿ����ȡһ��ÿ��ȡ������ĸ���Ϊ![]() ��
��
![]() ������һ��ȡ������ĸ���Ϊ
������һ��ȡ������ĸ���Ϊ![]() ���ʢ���ȷ���ʴ�Ϊ�٢ڢ�.
���ʢ���ȷ���ʴ�Ϊ�٢ڢ�.

 һ����ʦ�����Ծ�ϵ�д�
һ����ʦ�����Ծ�ϵ�д� �����Ծ���Ԫ���Ծ�ϵ�д�
�����Ծ���Ԫ���Ծ�ϵ�д�����Ŀ��ij�̳�Ϊ���˽�˿͵Ĺ�����Ϣ��������̳��ռ���![]() λ�˿��������������±���
λ�˿��������������±���
һ�ι�����λ��Ԫ�� |
|
|
|
|
|
�˿����� |
|
|
|
|
|
ͳ�ƽ����ʾ![]() λ�˿��й�������
λ�˿��й�������![]() Ԫ�Ĺ˿�ռ
Ԫ�Ĺ˿�ռ![]() �����̳�ÿ�մ�Լ��
�����̳�ÿ�մ�Լ��![]() ���˿ͣ�Ϊ�������̳����۶�ȣ���һ�ι��ﲻ����
���˿ͣ�Ϊ�������̳����۶�ȣ���һ�ι��ﲻ����![]() Ԫ�Ĺ˿ͷ��ż���Ʒ.
Ԫ�Ĺ˿ͷ��ż���Ʒ.
������ȷ��![]() ��
�� ![]() ��ֵ��������ÿ��Ӧ������Ʒ��������
��ֵ��������ÿ��Ӧ������Ʒ��������
��������![]() ��ǰȥ���̳�������ü���Ʒ������
��ǰȥ���̳�������ü���Ʒ������![]() �ķֲ�������ѧ����.
�ķֲ�������ѧ����.

