题目内容
22.(本小题满分10分)选修4—1:几何证明选讲
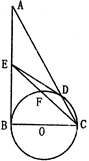
如图所示,AB为⊙O的直径,BC、CD为⊙O′的切线,B、D为切点
(1)求证:AD∥OC;
(2)若⊙O的半径为1,求AD·OC的值.
1)如图,连接BD、OD
∵CB、CD是⊙O的两条切线
∴BD⊥OC,∴∠2+∠3=90°
又AB为⊙O直径,∴AD⊥PB,∠1+∠2=90°
∴∠1=∠3,∴AD∥OC
(2)AO=OD,则∠1=∠A=∠3
∴Rt△BAD∽Rt△ODC,AD•••OC=AB•OD=2
∵CB、CD是⊙O的两条切线
∴BD⊥OC,∴∠2+∠3=90°
又AB为⊙O直径,∴AD⊥PB,∠1+∠2=90°
∴∠1=∠3,∴AD∥OC
(2)AO=OD,则∠1=∠A=∠3
∴Rt△BAD∽Rt△ODC,AD•••OC=AB•OD=2
略

练习册系列答案
相关题目
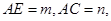
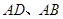 为方程
为方程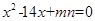 的两根
的两根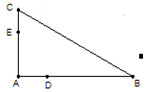
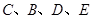 四点共圆
四点共圆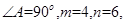 求
求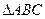 的角平分线
的角平分线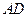 的延长线交它的外接圆于点
的延长线交它的外接圆于点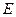 .
.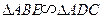 ;
;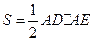 ,求
,求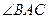 的大小.
的大小.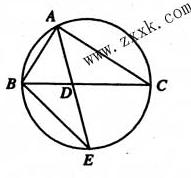
 为极点,
为极点, 轴的正半轴为极轴,已知点
轴的正半轴为极轴,已知点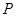 的直角坐标为
的直角坐标为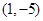 ,点
,点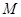 的极坐标为
的极坐标为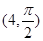 ,若直线
,若直线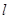 过点
过点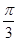 ,圆
,圆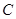 以
以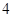 为半径。
为半径。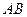 是圆
是圆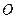 的直径,
的直径,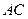 是弦,
是弦,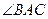 的平分线
的平分线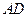 交圆
交圆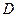 ,
,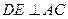 ,交
,交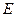 ,
,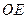 交
交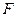 。
。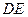 是圆
是圆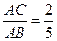 ,求
,求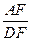 的值。
的值。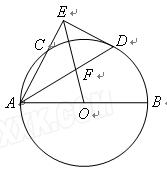
 的割线
的割线 交
交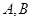 两点,割线
两点,割线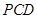 经过圆心,已知
经过圆心,已知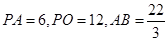 ,则
,则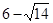 C.
C.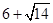 D.8
D.8
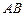 、
、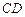 是圆
是圆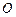 的两条弦,且
的两条弦,且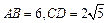 ,求线段
,求线段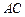 的长度.
的长度.