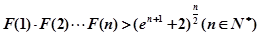题目内容
某连锁分店销售某种商品,每件商品的成本为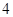 元,并且每件商品需向总店交
元,并且每件商品需向总店交 元的管理费,预计当每件商品的售价为
元的管理费,预计当每件商品的售价为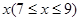 元时,一年的销售量为
元时,一年的销售量为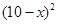 万件.
万件.
(1)求该连锁分店一年的利润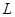 (万元)与每件商品的售价
(万元)与每件商品的售价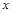 的函数关系式
的函数关系式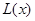 ;
;
(2)当每件商品的售价为多少元时,该连锁分店一年的利润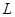 最大,并求出
最大,并求出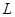 的最大值.
的最大值.
(I) .
.
(II)当 每件商品的售价为7元时,该连锁分店一年的利润
每件商品的售价为7元时,该连锁分店一年的利润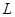 最大,最大值为
最大,最大值为 万元;
万元;
当 每件商品的售价为
每件商品的售价为 元时,该连锁分店一年的利润
元时,该连锁分店一年的利润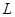 最大,最大值为
最大,最大值为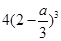 万元.
万元.
解析试题分析:(I)由题意,该连锁分店一年的利润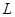 (万元)与售价
(万元)与售价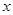 的函数关系式为
的函数关系式为 .
.
(II)通过确定 ,求导数得到
,求导数得到 ,
,
令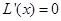 ,求得驻点,根据
,求得驻点,根据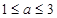 ,
, .讨论
.讨论
①当 时,②当
时,②当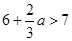 ,
, 时,导数值的正负,求得最大值.
时,导数值的正负,求得最大值.
试题解析:
(I)由题意,该连锁分店一年的利润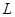 (万元)与售价
(万元)与售价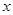 的函数关系式为
的函数关系式为 .
.
(II) ,
,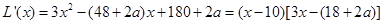 ,
,
令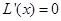 ,得
,得 或
或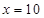 ,
,
因为,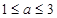 ,所以,
,所以, .
.
①当 时,
时, ,
,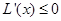 ,
, 是单调递减函数.
是单调递减函数.
故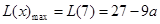 10分
10分
②当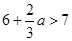 ,即
,即 时,
时,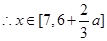 时,
时, ;
; 时,
时,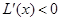
 在
在 上单调递增;在
上单调递增;在 上单调递减,
上单调递减,
故
答:当 每件商品的售价为7元时,该连锁分店一年的利润
每件商品的售价为7元时,该连锁分店一年的利润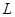 最大,
最大,
最大值为 万元;
万元;
当 每件商品的售价为
每件商品的售价为 元时,该连锁分店一年的利润
元时,该连锁分店一年的利润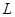 最大,最大值为
最大,最大值为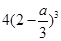 万元.
万元.
考点:生活中的优化问题举例,应用导数研究函数的单调性、最值.

练习册系列答案
相关题目
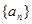 的前n项和为Sn,对一切正整数n,点
的前n项和为Sn,对一切正整数n,点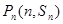 在函数
在函数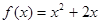 的图像上,且过点
的图像上,且过点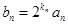 ,求数列
,求数列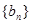 的前n项和Tn.
的前n项和Tn.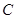 :
: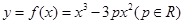 .
.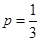 时,求曲线
时,求曲线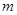 的两条直线与曲线
的两条直线与曲线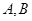 两点,求证:
两点,求证: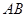 中点
中点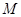 在曲线
在曲线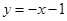 ,求
,求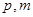 的值.
的值.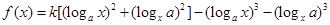 ,
,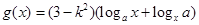 ,(其中
,(其中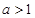 ),设
),设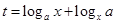 .
.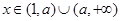 时,试将
时,试将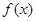 表示成
表示成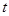 的函数
的函数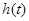 ,并探究函数
,并探究函数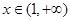 时,若存在
时,若存在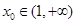 ,使
,使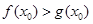 成立,试求
成立,试求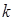 的范围.
的范围. .
.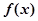 在区间
在区间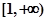 单调递增,求
单调递增,求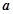 的最小值;
的最小值;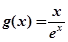 ,对
,对 ,使
,使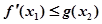 成立,求
成立,求 的范围.
的范围. (
( ,
,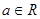 ),
), .
.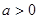 时,对于任意不相等的两个正实数
时,对于任意不相等的两个正实数 、
、 ,均有
,均有 成立;
成立;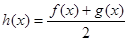 ,
,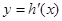 在
在 上单调递增,求实数
上单调递增,求实数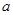 的取值范围;
的取值范围; .
. 的前
的前 项和为
项和为 ,已知
,已知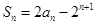 (n∈N*).
(n∈N*).
 ,数列
,数列 的前
的前 项和为
项和为 .利用(2)的结论证明:当n∈N*且n≥2时,
.利用(2)的结论证明:当n∈N*且n≥2时, .
.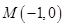 、
、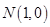 ,点
,点 为坐标平面内的动点,满足
为坐标平面内的动点,满足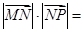
 .
.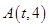 是动点
是动点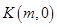 是
是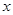 轴上的一动点,试讨论直线
轴上的一动点,试讨论直线 与圆
与圆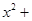
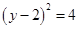 的位置关系.
的位置关系.
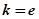 ,试确定函数
,试确定函数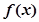 的单调区间;
的单调区间;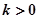 且对任意
且对任意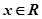 ,
,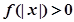 恒成立,试确定实数
恒成立,试确定实数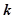 的取值范围;
的取值范围;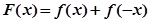 ,求证:
,求证: