题目内容
3.曲线y=ax2在点x=1处的切线的倾斜角不小于$\frac{π}{4}$,则a的取值范围(-∞,0)∪[$\frac{1}{2}$,+∞).分析 求出函数的导数,求得切线的斜率,由$\frac{π}{4}$≤α<$\frac{π}{2}$或$\frac{π}{2}$<α<π,运用正切函数的图象和性质,可得a的范围.
解答 解:y=ax2的导数为y′=2ax,
曲线y=ax2在点x=1处的切线斜率为k=2a,
由题意可得倾斜角α≥$\frac{π}{4}$,
则$\frac{π}{4}$≤α<$\frac{π}{2}$或$\frac{π}{2}$<α<π,
即有tanα≥1或tanα<0,
即2a≥1或2a<0,
解得a≥$\frac{1}{2}$或a<0.
故答案为:(-∞,0)∪[$\frac{1}{2}$,+∞).
点评 本题考查导数的运用:求切线的斜率,主要考查导数的几何意义,注意运用正切函数的图象和性质.

练习册系列答案
相关题目
11.设函数f(x)=ln(1+x),g(x)=$\frac{ax}{1+x}$(x≥0),若f(x)≥g(x)恒成立,则a的取值范围是( )
| A. | a≤2 | B. | a≥2 | C. | a≤1 | D. | a≥1 |
18.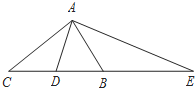 在△ABC中,∠BAC=90°,D是BC边的中点,AE⊥AD,AE交CB的延长线于E,则下面结论中正确的是( )
在△ABC中,∠BAC=90°,D是BC边的中点,AE⊥AD,AE交CB的延长线于E,则下面结论中正确的是( )
 在△ABC中,∠BAC=90°,D是BC边的中点,AE⊥AD,AE交CB的延长线于E,则下面结论中正确的是( )
在△ABC中,∠BAC=90°,D是BC边的中点,AE⊥AD,AE交CB的延长线于E,则下面结论中正确的是( )| A. | △AED∽△ACB | B. | △AEB∽△ACD | C. | △BAE∽△ACE | D. | △AEC∽△DAC |
8.执行如图所示的程序框图,如果输入a=1,b=3,则输出的a的值为( )


| A. | 7 | B. | 9 | C. | 10 | D. | 13 |