题目内容
【题目】已知函数![]() .
.
(Ⅰ)讨论![]() 的单调性;
的单调性;
(Ⅱ)当![]() 存在三个不同的零点时,求实数a的取值范围.
存在三个不同的零点时,求实数a的取值范围.
【答案】(1)见解析;(2)![]()
【解析】
(1)先对函数求导,求导后令![]() ,由判别式结合二次函数根的分布求解原函数的单调区间;
,由判别式结合二次函数根的分布求解原函数的单调区间;
(2)由(1)求出的函数单调性可使![]() 存在三个不同的零点时实数a的取值范围
存在三个不同的零点时实数a的取值范围
解:(1)由![]() ,得
,得![]() ,
,
当![]() 时,
时,![]() ,所以
,所以 ![]() 在
在![]() 上单调递增
上单调递增
令![]() ,则
,则![]() ,
,
当![]() ≤0时,即
≤0时,即![]() ≥
≥![]() ,则
,则![]() ≤0,即
≤0,即![]() ≤0,
≤0,
所以![]() 在
在![]() 上单调递减;
上单调递减;
当![]() ,即
,即![]() 时,
时,
由![]() ,解得
,解得![]()
当![]() 时,
时,![]() ,则
,则 ![]() 在
在![]() 上单调递增,
上单调递增,
当![]() 时,
时,![]() ,
,
当 ![]() 时,
时,![]() ,即
,即 ![]() ,则
,则![]() 在
在![]() 和
和![]() 上单调递减;
上单调递减;
当![]() 时,
时,![]() ,即
,即 ![]() ,则
,则![]() 在
在![]() 上单调递增;
上单调递增;
综上,当![]() ≤0时,
≤0时,![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,
时,![]() 在
在![]() 和
和![]() 上单递减,在
上单递减,在![]() 上单调递增;
上单调递增;
当![]() ≥
≥![]() 时,
时,![]() 在
在![]() 上单调递减;
上单调递减;
(2)由(1)可当![]() ≥
≥![]() 时,
时,![]() 在
在![]() 上单调递减,当
上单调递减,当![]() ≤0时,
≤0时,![]() 在
在![]() 上单调递增,不可能有3个零点,
上单调递增,不可能有3个零点,
所以![]() 时,
时,![]() 在
在![]() 和
和![]() 上单递减,在
上单递减,在![]() 上单调递增,
上单调递增,
因为![]() ,
,![]() ,所以
,所以![]() ,
,![]()
![]() ,
,![]() ,
,
令![]() ,则
,则![]() ,
,
令![]() ,则
,则![]() 在
在 ![]() 上为增函数,
上为增函数,
由![]() ,得
,得![]() ,所以当
,所以当![]() 时,
时,![]() ,
,
所以 ![]() 在
在![]() 上单调递减,
上单调递减,
所以![]() ,
,
所以![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() ,
,
所以![]() ,
,
由零点存在性定理可知,![]() 在区间
在区间![]() 上有一个根,设为
上有一个根,设为![]() ,
,
又![]() ,得
,得![]() ,
,
而![]() ,所以
,所以![]() 是函数
是函数![]() 的另一个零点,
的另一个零点,
所以当![]() 时,
时,![]() 有3个零点,
有3个零点,
所以实数a的取值范围为![]()

【题目】已知椭圆![]() 的焦点在
的焦点在![]() 轴上,中心在坐标原点,抛物线
轴上,中心在坐标原点,抛物线![]() 的焦点在
的焦点在![]() 轴上,顶点在坐标原点,在
轴上,顶点在坐标原点,在![]() 、
、![]() 上各取两个点,将其坐标记录于表格中:
上各取两个点,将其坐标记录于表格中:
|
|
|
|
|
|
|
|
|
|
(1)求![]() 、
、![]() 的标准方程;
的标准方程;
(2)已知定点![]() ,
,![]() 为抛物线
为抛物线![]() 上的一动点,过点
上的一动点,过点![]() 作抛物线
作抛物线![]() 的切线交椭圆
的切线交椭圆![]() 于
于![]() 、
、![]() 两点,求
两点,求![]() 面积的最大值.
面积的最大值.
【题目】共享单车进驻城市,绿色出行引领时尚.某市有统计数据显示,2020年该市共享单车用户年龄等级分布如图1所示,一周内市民使用单车的频率分布扇形图如图2所示.若将共享单车用户按照年龄分为“年轻人”(20岁-39岁)和“非年轻人”(19岁及以下或者40岁及以上)两类,将一周内使用的次数为6次或6次以上的称为“经常使用单车用户”,使用次数为5次或不足5次的称为“不常使用单车用户”.已知在“经常使用单车用户”中有![]() 是“年轻人”.
是“年轻人”.
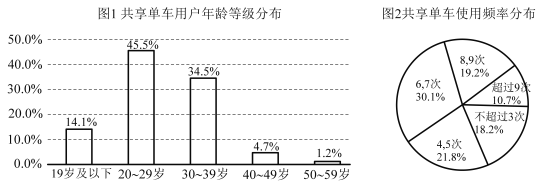
(1)现对该市市民进行“经常使用共享单车与年龄关系”的调查,采用随机抽样的方法,抽取一个容量为200的样本,请你根据图表中的数据,补全下列![]() 列联表,并根据列联表的独立性检验,判断是否有85%的把握认为经常使用共享单车与年龄有关?
列联表,并根据列联表的独立性检验,判断是否有85%的把握认为经常使用共享单车与年龄有关?
年轻人 | 非年轻人 | 合计 | |
经常使用单车用户 | 120 | ||
不常使用单车用户 | 80 | ||
合计 | 160 | 40 | 200 |
使用共享单车情况与年龄列联表
(2)将(1)中频率视为概率,若从该市市民中随机任取3人,设其中经常使用共享单车的“非年轻人”人数为随机变量![]() ,求
,求![]() 的分布列与期望.
的分布列与期望.
参考数据:独立性检验界值表
| 0.15 | 0.10 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
其中,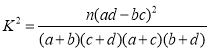 ,
,![]()