Question

【题目】已知矩形ABCD与直角梯形ABEF，∠DAF=∠FAB=90°，点G为DF的中点，AF=EF= ，P在线段CD上运动．
（1）证明：BF∥平面GAC；
（2）当P运动到CD的中点位置时，PG与PB长度之和最小，求二面角P﹣CE﹣B的余弦值．

Answer 1

【答案】
（1）证明：连接BD交AC于M，连MG，M为BD的中点．

∴MG为△BFD的中位线，

∴GM∥BF，而BF平面GAC，MG平面GAC，

∴BF∥平面GAC

（2）解：延迟AD至N，使DN=DG，连PN，PG，则△PDG≌△PDN，∴PG=PN

当P、B、N三点共线时，PG与PB长度之和最小，即PG与PB长度之和最小

∵P为CD中点，∴AD=DN．

在△ADF中，AD2+AF2=4DG2=4AD2，∴AD=1

AD，AB，AF两两垂直，如图建立空间直角坐标系，

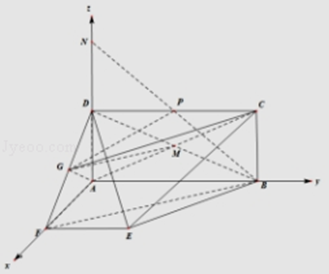
∴D（0，0，1），E（ ， ，0），B（0，2 ，0），C（0，2 ，1），

∴ =（ ，﹣ ，﹣1）， =（0，0，1）， =（0，2 ，0）

设 =（x，y，z）为平面PCE的一个法向量，

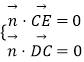∴ 即 ，

令x=1，y=0，z= ， ．

同理可得平面BCE的一个法向量 =（1，1，0），

设二面角P﹣CE﹣B的大小为θ，θ为钝角，

∴cosθ=﹣ = ，

∴求二面角P﹣CE﹣B的余弦值：﹣

【解析】（1）连接BD交AC于M，连MG，M为BD的中点，证明GM∥BF，即可证明BF∥平面GAC．（2）延迟AD至N，使DN=DG，连PN，PG，说明当P、B、N三点共线时，PG与PB长度之和最小，AD，AB，AF两两垂直，如图建立空间直角坐标系，求出相关点的坐标，求出平面PCE的一个法向量，平面BCE的一个法向量，利用空间向量的数量积求解二面角P﹣CE﹣B的余弦值．
【考点精析】利用直线与平面平行的判定对题目进行判断即可得到答案，需要熟知平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行；简记为：线线平行，则线面平行．