题目内容
【题目】设Sn为数列{an}的前n项和，已知
，对任意n∈N*，都有2Sn＝（n+1）an．
（1）求数列{an}的通项公式；
（2）若数列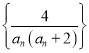
的前项和为Tn，求Tn的取值范围．
【答案】（1）an＝2n（2）
．
【解析】
（1）在2Sn＝（n+1）an中，将
代
可得：2Sn﹣1＝（n+1﹣1）an﹣1，两式作差可得：
，对赋值，再利用累乘法计算可得：
，问题得解。
（2）利用（1）中结论，整理
可得：
，利用裂项求和可得：
，问题得解。
解：（1）Sn为数列{an}的前n项和，已知
，对任意n∈N*，
都有2Sn＝（n+1）an．①
当n≥2时，2Sn﹣1＝（n+1﹣1）an﹣1．②
①﹣②得：，
…，
则：
，
所以：，
整理得：an＝2n（首项符合通项），
故：an＝2n．
（2）由已知条件：
，
故：
，
，
当
时，
故：．
开心快乐假期作业暑假作业西安出版社系列答案
名题训练系列答案
【题目】（Ⅰ）如表所示是某市最近5年个人年平均收入表节选．求y关于x的回归直线方程，并估计第6年该市的个人年平均收入（保留三位有效数字）．
年份x | 1 | 2 | 3 | 4 | 5 |
收入y（千元） | 21 | 24 | 27 | 29 | 31 |
其中
，
，
附1：
= ，=﹣
（Ⅱ）下表是从调查某行业个人平均收入与接受专业培训时间关系得到2×2列联表：
受培时间一年以上 | 受培时间不足一年 | 总计 | |
收入不低于平均值 | 60 | 20 | |
收入低于平均值 | 10 | 20 | |
总计 | 100 |
完成上表，并回答：能否在犯错概率不超过0.05的前提下认为“收入与接受培训时间有关系”．
附2：
P（K2≥k0） | 0.50 | 0.40 | 0.10 | 0.05 | 0.01 | 0.005 |
k0 | 0.455 | 0.708 | 2.706 | 3.841 | 6.635 | 7.879 |
附3：
K2=．（n=a+b+c+d）
【题目】袋子中有四张卡片，分别写有“瓷、都、文、明”四个字，有放回地从中任取一张卡片，将三次抽取后“瓷”“都”两个字都取到记为事件
，用随机模拟的方法估计事件发生的概率.利用电脑随机产生整数0，1，2，3四个随机数，分别代表“瓷、都、文、明”这四个字，以每三个随机数为一组，表示取卡片三次的结果，经随机模拟产生了以下18组随机数：
232 | 321 | 230 | 023 | 123 | 021 | 132 | 220 | 001 |
231 | 130 | 133 | 231 | 031 | 320 | 122 | 103 | 233 |
由此可以估计事件发生的概率为（ ）
A. 
B. 
C. 
D. 
【题目】某校进行理科、文科数学成绩对比，某次考试后，各随机抽取100名同学的数学考试成绩进行统计，其频率分布表如下.
分组 | 频数 | 频率 | 分组 | 频数 | 频率 | |
[135,150] | 8 | 0.08 | [135,150] | 4 | 0.04 | |
[120,135） | 17 | 0.17 | [120,135） | 18 | 0.18 | |
[105,120） | 40 | 0.4 | [105,120） | 37 | 0.37 | |
[90,105） | 21 | 0.21 | [90,105） | 31 | 0.31 | |
[75,90） | 12 | 0. 12 | [75,90） | 7 | 0.07 | |
[60,75） | 2 | 0.02 | [60,75） | 3 | 0.03 | |
总计 | 100 | 1 | 总计 | 100 | 1 |
理科 文科
（Ⅰ）根据数学成绩的频率分布表，求文科数学成绩的中位数的估计值；（精确到0.01）
（Ⅱ）请填写下面的列联表，并根据列联表判断是否有90%的把握认为数学成绩与文理科有关：
数学成绩 | 数学成绩<120分 | 合计 | |
理科 | |||
文科 | |||
合计 | 200 |
参考公式与临界值表： 
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 | |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
