题目内容
【题目】如图，已知PA垂直于矩形ABCD所在的平面，M，N分别是AB，PC的中点，若∠PDA=45°，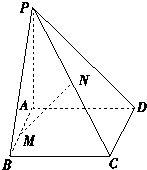 
（1）求证：MN∥平面PAD且MN⊥平面PCD．
（2）探究矩形ABCD满足什么条件时，有PC⊥BD．
【答案】
（1）证明：如图，取PD的中点E，连接AE，NE．
E、N分别为PD，PC的中点，
所以：EN∥CD， 
，
又M为AB的中点，
所以： 
，AM∥CD，
EN∥AM，EN=AM，
所以：四边形AMNE为平行四边形．
MN∥AE，
所以：MN∥平面PAD，
PA⊥平面ABCD，∠PDA=45°，
所以：△PAD是等腰直角三角形，
所以：AE⊥PD．
又CD⊥AD，CD⊥PA，AD交PA于A，
所以：CD⊥平面PAD，AE平面PAD，
所以：CD⊥AE，
又CD交PD于D，
所以：AE⊥平面PCD，
则：MN⊥平面PCD
（2）若 PC⊥BD，又PA⊥BD，PA交PC于P，
所以：BD⊥平面PAC，
所以：BD⊥AC，即矩形ABCD的对角线互相垂直．
此时矩形为正方形．
即当矩形ABCD为正方形时，满足PC⊥BD．
【解析】（1）利用三角形的中位线得到线线平行，进一步得到线面平行，利用线线垂直进一步转化成线面垂直．（2）利用线面垂直转化线线垂直，最后确定矩形是正方形．
【考点精析】认真审题，首先需要了解直线与平面平行的判定(平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行；简记为：线线平行，则线面平行)，还要掌握直线与平面垂直的判定(一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直；注意点：a)定理中的“两条相交直线”这一条件不可忽视；b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想)的相关知识才是答题的关键．
怎样学好牛津英语系列答案
【题目】某商场经销某商品，根据以往资料统计，顾客采用的付款期数
的分布列为：
| 1 | 2 | 3 | 4 | 5 |
| 0.4 | 0.2 | 0.2 | 0.1 | 0.1 |
商场经销该商品，可采用不同形式的分期付款，付款的期数
（单位： 
）与商场经销一件商品的利润
（单位：元）满足如下关系： 
（Ⅰ）若记事件“购买该商品的3位顾客中，至少有1位采用一次性全额付款方式”为
，试求事件
的概率
；
（Ⅱ）求商场经销一件商品的利润
的分布列及期望
．
