题目内容
13.5名运动员同时参加3项冠军争夺赛(每项比赛无并列冠军),获得冠军的可能种数为( )| A. | 35 | B. | 53 | C. | $A_5^3$ | D. | $C_5^3$ |
分析 根据题意,分析可得每一个人取得冠答案的机会相等,即每一项冠军有5种情况,由分步计数原理计算可得答案.
解答 解:根据题意,5名运动员同时参加3项冠军争夺赛,
则每一个人取得冠军的机会相等,即每一项冠军有5种情况,则获得冠军的可能种数为5×5×5=53,
故选:B.
点评 本题考查分步计数原理的应用,本题的易错点是不能正确的理解分步原理.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
1.已知集合$A=(-∞,\frac{1}{2}]$,函数y=ln(2x+1)的定义域为集合B,则A∩B=( )
| A. | $({-\frac{1}{2},\frac{1}{2}}]$ | B. | $({-\frac{1}{2},\frac{1}{2}})$ | C. | $({-∞,-\frac{1}{2}})$ | D. | $[{\frac{1}{2},+∞})$ |
8.阅读如图的程序框图.若输入n=1,则输出k的值为( )
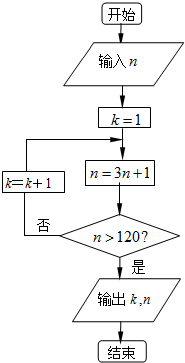

| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
18.若集合A={(x,y)||x-1|+$\sqrt{y-4}$=0},B={1,4},则下面选项正确的是( )
| A. | B⊆A | B. | A⊆B | C. | A=B | D. | A∩B=Φ |
14.已知a+b=4(a>0,b>0)则$\frac{1}{a}$+$\frac{4}{b}$的最小值是( )
| A. | $\frac{5}{2}$ | B. | $\frac{9}{2}$ | C. | $\frac{9}{4}$ | D. | 2 |