题目内容
【题目】如图，四棱锥P-ABCD中，侧面PAD是边长为2的等边三角形且垂直于底
， 
是
的中点。
（1）证明：直线
平面
；
（2）点
在棱
上，且直线
与底面
所成角为
，求二面角
的余弦值。
【答案】（1）见解析；（2）
【解析】试题分析：（1） 取
的中点
，连结
， 
，由题意证得
∥
，利用线面平行的判断定理即可证得结论；（2）建立空间直角坐标系，求得半平面的法向量： 
， 
，然后利用空间向量的相关结论可求得二面角
的余弦值为
．
试题解析：（1）取
中点
，连结
， 
．
因为
为
的中点，所以
, 
,由
得
，又
所以
．四边形
为平行四边形， 
．
又
， 
，故
（2）
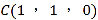
由已知得
,以A为坐标原点， 
的方向为x轴正方向， 
为单位长，建立如图所示的空间直角坐标系A-xyz,则
则
， 
， 
， 
，
,
则
因为BM与底面ABCD所成的角为45°，而
是底面ABCD的法向量，所以
， 
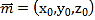
即（x-1）+y-z=0
又M在棱PC上，学|科网设
由①，②得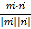
所以M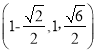
，从而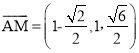
设
是平面ABM的法向量，则
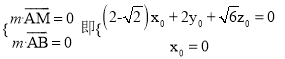
所以可取m=（0，-
，2）.于是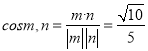
因此二面角M-AB-D的余弦值为
点睛:（1）求解本题要注意两点：①两平面的法向量的夹角不一定是所求的二面角，②利用方程思想进行向量运算，要认真细心、准确计算．
（2）设m，n分别为平面α，β的法向量，则二面角θ与<m，n>互补或相等，故有|cos θ|＝|cos<m，n>|=
．求解时一定要注意结合实际图形判断所求角是锐角还是钝角．
练习册系列答案
相关题目
