题目内容
从6名短跑运动员中选出4人参加4×100 m接力赛.试求满足下列条件的参赛方案各有多少种?
(1)甲不能跑第一棒和第四棒;
(2)甲不能跑第一棒,乙不能跑第四棒
(1)240;(2)252;
解析试题分析:(1)可优先考虑特殊元素甲,此时务必注意甲是否参赛,因此需分两类,甲参赛和甲不参赛,利用分类加法计数原理求解
(2)显然第一、四棒为特殊位置,与之相伴的甲、乙则为特殊元素,这时特殊元素与特殊位置的个数相等,利用特殊位置(元素)优先考虑的原则解之.
(1)优先考虑特殊元素甲,让其选位置,此时务必注意甲是否参赛,因此需分两类:
第1类,甲不参赛有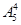 种排法;
种排法;
第2类,甲参赛,因只有两个位置可供选择,故有A种排法;其余5人占3个位置有A种排法,故有AA种方案.所以有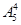 +
+
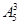 =240种参赛方案.
=240种参赛方案.
(2)优先考虑特殊位置.
第1类,乙跑第一棒有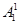
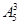 =60种排法;
=60种排法;
第2类,乙不跑第一棒有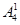
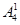
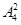 =192种排法.
=192种排法.
故共有60+192=252种参赛方案.
考点:排列组合,计数原理

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
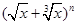 (其中
(其中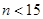 )的展开式中第
)的展开式中第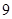 项,第
项,第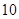 项,第
项,第 项的二项式系数成等差数列.
项的二项式系数成等差数列. 的值;
的值; 的展开式中前三项系数成等差数列,
的展开式中前三项系数成等差数列,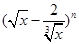 的展开式中,第5项的系数与第3项的系数之比是
的展开式中,第5项的系数与第3项的系数之比是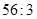 .
. 的值.
的值.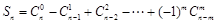 ,
,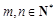 且
且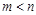 ,其中当
,其中当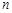 为偶数时,
为偶数时,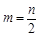 ;当
;当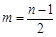 .
.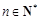 ,
,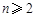 时,
时,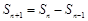 ;
;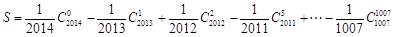 ,求
,求 的值.
的值.