题目内容
若 的展开式中前三项系数成等差数列,
的展开式中前三项系数成等差数列,
求:(1)展开式中含的一次幂的项;
(2)展开式中所有的有理项
(3)展开式中系数最大的项
(1)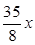 ;(2)
;(2)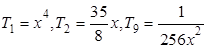 ;(3)
;(3)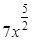 ,
,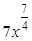 .
.
解析试题分析:由题意需先求出展开式中前三项的系数利用它们成等差数列求出n,(1)由项的展开式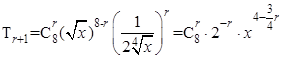 ,令x的指数为1,解出r的值,即可求得一次项;(2)由公式
,令x的指数为1,解出r的值,即可求得一次项;(2)由公式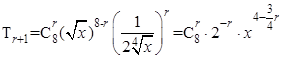 ,故可知r=0,4,8时,所得的项为有理项,代入求之即可;(3)展开式中系数最大的项满足这样的条件,比其前的项大,也比其后的项大,由此关系可得限制条件.解不等式求出r既得.
,故可知r=0,4,8时,所得的项为有理项,代入求之即可;(3)展开式中系数最大的项满足这样的条件,比其前的项大,也比其后的项大,由此关系可得限制条件.解不等式求出r既得.
解:由已知条件知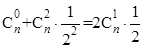 ,解得n=8.
,解得n=8.
(1)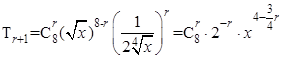 ,令
,令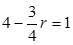 ,解得r=4.
,解得r=4.
∴x的一次幂的项为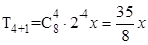 .
.
(2)令 ∈N(r≤8).则只有当r=0,4,8时,对应的项才为有理项,有理项分别为:
∈N(r≤8).则只有当r=0,4,8时,对应的项才为有理项,有理项分别为: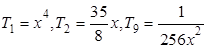 .
.
(3)设展开式中Tr+1项的系数最大,则: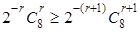 且
且 ⇒r=2或r=3,故展开式中系数最大项为:
⇒r=2或r=3,故展开式中系数最大项为: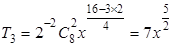 ,
,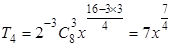 .
.
考点:二项式定理.

练习册系列答案
相关题目

 ,且(1-2x)n=a0+a1x+a2x2+a3x3+ +anxn.
,且(1-2x)n=a0+a1x+a2x2+a3x3+ +anxn.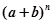 的展开式中,奇数项的二项式系数的和等于偶数项的二项式系数的和.
的展开式中,奇数项的二项式系数的和等于偶数项的二项式系数的和. ,其中
,其中 ,
, 的值为 ______
的值为 ______ 的值为 .
的值为 .