题目内容
设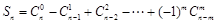 ,
,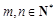 且
且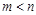 ,其中当
,其中当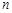 为偶数时,
为偶数时,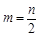 ;当
;当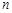 为奇数时,
为奇数时,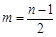 .
.
(1)证明:当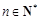 ,
,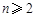 时,
时,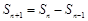 ;
;
(2)记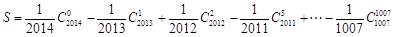 ,求
,求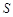 的值.
的值.
(1)详见解析,(2)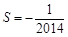 .
.
解析试题分析:(1)利用组合数性质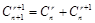 进行化简.根据奇偶性,对
进行化简.根据奇偶性,对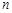 进行分类讨论,这不增加难度,仅是便于表示.
进行分类讨论,这不增加难度,仅是便于表示. 
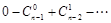 ,规律清晰,易于归纳(2)利用组合数性质
,规律清晰,易于归纳(2)利用组合数性质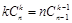 进行化简.
进行化简. 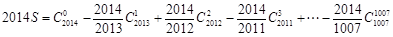
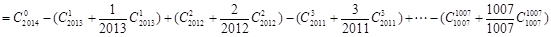
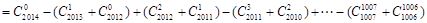 =
=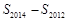 .
.
再根据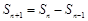 得周期
得周期 ,从而
,从而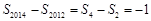 ,
,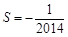 .
.
试题解析:解:(1)当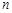 为奇数时,
为奇数时,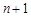 为偶数,
为偶数,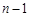 为偶数,
为偶数,
∵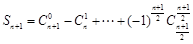 ,
,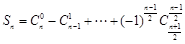 ,
,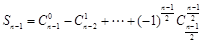 ,
,
∴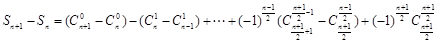
=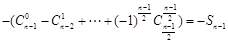 .
.
∴当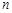 为奇数时,
为奇数时,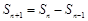 成立 5分
成立 5分
同理可证,当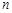 为偶数时,
为偶数时, 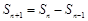 也成立. 6分
也成立. 6分
(2)由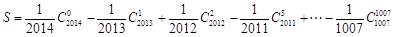 ,得
,得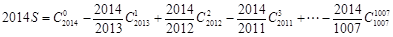
=
=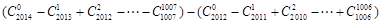
=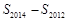 . 9分
. 9分
又由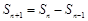 ,得
,得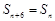 ,
,
所以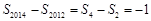 ,
,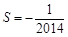 . 10分
. 10分
考点:组合数性质

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
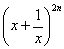 展开式中,第四项与第六项的系数相等。求
展开式中,第四项与第六项的系数相等。求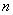 ,并求展开式中的常数项;
,并求展开式中的常数项;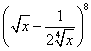 展开式中的所有的有理项。
展开式中的所有的有理项。 的展开式中的常数项是_____________.
的展开式中的常数项是_____________.