题目内容
已知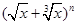 (其中
(其中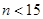 )的展开式中第
)的展开式中第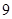 项,第
项,第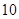 项,第
项,第 项的二项式系数成等差数列.
项的二项式系数成等差数列.
(1)求 的值;
的值;
(2)写出它展开式中的所有有理项.
(1)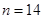 ;(2)
;(2)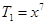 、
、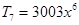 、
、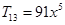 .
.
解析试题分析:(1)先写出这三项的二项式系数,然后根据它们成等差,建立等式,解出 的值,注意系数与二项式系数是两个不同的概念,当然此题的结果是一样的,另外注意
的值,注意系数与二项式系数是两个不同的概念,当然此题的结果是一样的,另外注意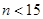 的限制条件;(2)首先要确定哪些项为有理项,这要紧扣有理项的概念,即字母
的限制条件;(2)首先要确定哪些项为有理项,这要紧扣有理项的概念,即字母 的指数是整数,这样通过通项公式,确定
的指数是整数,这样通过通项公式,确定 取哪些值能保证
取哪些值能保证 的指数为整数,然后再具体求出各项即可.
的指数为整数,然后再具体求出各项即可.
试题解析:(1)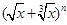 (其中
(其中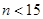 )的展开式中第
)的展开式中第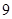 项,第
项,第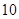 项,第
项,第 项的二项式系数分别
项的二项式系数分别
是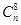 ,
,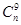 ,
,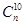 ,依题意得
,依题意得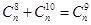 ,写成:
,写成: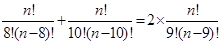
化简得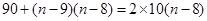 ,即:
,即: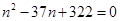 ,解得
,解得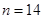 或
或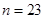 ,因为
,因为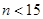 ,所以
,所以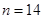 . 5分
. 5分
(2)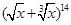 展开式的通项
展开式的通项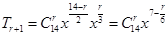 (
(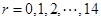 )
)
展开式中的有理项当且仅当 是
是 的倍数,因为
的倍数,因为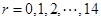 ,符合条件的只有
,符合条件的只有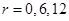 ,
,
所以展开式中的有理项共 项是:
项是: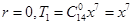 ;
;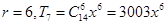 ;
;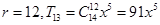 . 12分
. 12分
考点:二项式定理及应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的展开式中
的展开式中 的系数是80,则实数a的值是
的系数是80,则实数a的值是 
 ,且(1-2x)n=a0+a1x+a2x2+a3x3+ +anxn.
,且(1-2x)n=a0+a1x+a2x2+a3x3+ +anxn.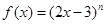 展开式的二项式系数和为512,且
展开式的二项式系数和为512,且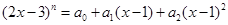
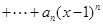 .
.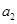 的值; (2)求
的值; (2)求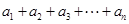 的值.
的值.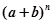 的展开式中,奇数项的二项式系数的和等于偶数项的二项式系数的和.
的展开式中,奇数项的二项式系数的和等于偶数项的二项式系数的和. 个球(其中
个球(其中 个白球,1个黑球)的口袋中取出
个白球,1个黑球)的口袋中取出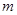 个球
个球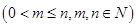 ,共有
,共有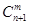 种取法,这
种取法,这 种取法,另一类是取出的
种取法,另一类是取出的 种取法,由此可得等式:
种取法,由此可得等式: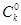 ·
·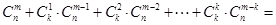 .
.  的展开式中的常数项是_____________.
的展开式中的常数项是_____________.