题目内容
【题目】在平面直角坐标系中,两点P1(x1 , y1),P2(x2 , y2)间的“L﹣距离”定义为|P1P2|=|x1﹣x2|+|y1﹣y2|.现将边长为1的正三角形ABC按如图所示的方式放置,其中顶点A与坐标原点重合.记边AB所在直线的斜率为k,0≤k≤ ![]() .求:当|BC|取最大值时,边AB所在直线的斜率的值.
.求:当|BC|取最大值时,边AB所在直线的斜率的值. 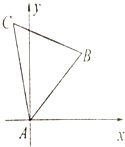
【答案】解:设边AB所在直线的倾斜角为θ,则 ![]()
∴ ![]()
∴|BC|=|cosθ﹣cos(θ+ ![]() )|+|sinθ﹣sin(θ+
)|+|sinθ﹣sin(θ+ ![]() )|
)|
= 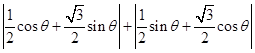
= ![]()
∵ ![]() ,
,
∴|BC|= ![]() =
= ![]() sin(θ+
sin(θ+ ![]() )
)
∵ ![]() ,
,
∴当θ+ ![]() =
= ![]() 时,即θ=
时,即θ= ![]() 时,|BC|取得最大值
时,|BC|取得最大值 ![]() ,
,
此时 ![]() ,∵
,∵ 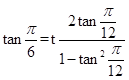 (或由
(或由 ![]() 求k)∴
求k)∴ ![]() ,
,
∴ ![]() .
.
【解析】设边AB所在直线的倾斜角为θ,则 ![]() ,利用L﹣距离的定义,表示|BC|,结合辅助角公式,求出取最大值时,边AB所在直线的斜率的值.
,利用L﹣距离的定义,表示|BC|,结合辅助角公式,求出取最大值时,边AB所在直线的斜率的值.
【考点精析】本题主要考查了直线的斜率的相关知识点,需要掌握一条直线的倾斜角α(α≠90°)的正切值叫做这条直线的斜率,斜率常用小写字母k表示,也就是 k = tanα才能正确解答此题.

练习册系列答案
相关题目