题目内容
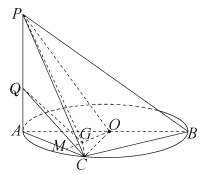
【题目】如图，点
在以
为直径的圆
上， 
垂直与圆
所在平面， 
为
的垂心.
（1）求证：平面
平面
；
（2）若
，点
在线段
上，且
，求三棱锥
的体积.
【答案】（1）见解析;（2）
.
【解析】试题分析：（1）延长
交
于点
，先证明
，再证明
平面
，即
平面
；（2）由（1）知
平面
，所以
就是点
到平面
的距离，再证明
，从而利用棱锥的体积公式可得结果.
试题解析：（1）如图，延长
交
于点
.
因为
为
的重心，所以
为
的中点.
因为
为
的中点，所以
.
因为
是圆
的直径，所以
，所以
.
因为
平面
， 
平面
，所以
.
又
平面
， 
平面
， 
，
所以
平面
，即
平面
.
又
平面
，所以平面
平面
.
（2）解：由（1）知
平面
，
所以
就是点
到平面
的距离.
由已知可得， 
，
所以
为正三角形，
所以
.又点
为
的重心，
所以
.
故点
到平面
的距离为
.
所以
.
练习册系列答案
名师伴你成长课时同步学练测系列答案
相关题目
【题目】十八届五中全会公报指出：努力促进人口均衡发展，坚持计划生育的基本国策，完善人口发展战略，全面实施一对夫妇可生育两个孩子的政策，提高生殖健康、妇幼保健、托幼等公共服务水平．为了解适龄公务员对放开生育二胎政策的态度，某部门随机调查了100位30到40岁的公务员，得到情况如下表：
男公务员 | 女公务员 | |
生二胎 | 40 | 20 |
不生二胎 | 20 | 20 |
（1）是否有95%以上的把握认为“生二胎与性别有关”，并说明理由；
（2）把以上频率当概率，若从社会上随机抽取3位30到40岁的男公务员，记其中生二胎的人数为X，求随机变量X的分布列，数学期望．
附：K2= 
P（K2≥k0） | 0.050 | 0.010 | 0.001 |
k0 | 3.841 | 6.635 | 10.828 |
