题目内容
定义在(0,+∞)上的增函数f(x)满足:对任意的x>0,y>0都有f(xy)=f(x)+f(y),
(1)求f(1)的值;
(2)请举出一个符合条件的函数f(x);
(3)若f(2)=1,解不等式f(x2-5)-f(x)<2.
(1)求f(1)的值;
(2)请举出一个符合条件的函数f(x);
(3)若f(2)=1,解不等式f(x2-5)-f(x)<2.
(1)令x=y=1,
则f(1)=f(1)+f(1)⇒f(1)=0.
(2)y=logax(a>1)
(3)f(2)=1
∴2=1+1=f(2)+f(2)=f(4)
∴原不等式等价于f(x2-5)<f(x)+f(4)=f(4x),
因为f(x)是定义在(0,+∞)上的增函数,所以
⇒
⇒
<x<5
所以原不等式解集是(
,5)
则f(1)=f(1)+f(1)⇒f(1)=0.
(2)y=logax(a>1)
(3)f(2)=1
∴2=1+1=f(2)+f(2)=f(4)
∴原不等式等价于f(x2-5)<f(x)+f(4)=f(4x),
因为f(x)是定义在(0,+∞)上的增函数,所以
|
⇒
|
| 5 |
所以原不等式解集是(
| 5 |

练习册系列答案
相关题目
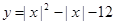 两个零点的差的绝对值是( ).
两个零点的差的绝对值是( ).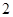

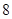
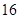





 满足
满足
 ,求
,求 ;又若
;又若 ,求
,求 ;
; ,使得
,使得 ,求函数
,求函数