题目内容
已知函数f(x)在定义域(0,+∞)上单调递增,且满足f(xy)=f(x)+f(y).
(1)证明:f(
)=f(x)-f(y);
(2)已知f(3)=1,且f(a)>f(a-1)+2,求a的取值范围.
(1)证明:f(
| x |
| y |
(2)已知f(3)=1,且f(a)>f(a-1)+2,求a的取值范围.
(1)∵对一切x,y>0满足f(x)+f(y)=f(x•y),
∴f(
)+f(y)=f(
×y)=f(x)
因此,满足 f(
)=f(x)-f(y),
(2)∵f(3)=1,∴2=f(3)+f(3)=f(9);
∵f(x)是定义在(0,+∞)上的增函数,
∴f(a)>f(a-1)+2,?
?
?1<a<
,
故a的取值范围(1,
)
∴f(
| x |
| y |
| x |
| y |
因此,满足 f(
| x |
| y |
(2)∵f(3)=1,∴2=f(3)+f(3)=f(9);
∵f(x)是定义在(0,+∞)上的增函数,
∴f(a)>f(a-1)+2,?
|
|
?1<a<
| 9 |
| 8 |
故a的取值范围(1,
| 9 |
| 8 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 上恒有f(x)
上恒有f(x) -3成立,求实数a 的取值范围.
-3成立,求实数a 的取值范围.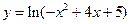 的单调递减区间为 .
的单调递减区间为 .