题目内容
是否存在实数a使函数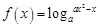 在
在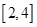 上是增函数?若存在求出a的值,若不存在,说明理由。
上是增函数?若存在求出a的值,若不存在,说明理由。
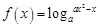 在
在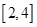 上是增函数?若存在求出a的值,若不存在,说明理由。
上是增函数?若存在求出a的值,若不存在,说明理由。存在实数a>1使得函数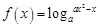 在
在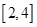 上是增函数
上是增函数
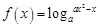 在
在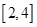 上是增函数
上是增函数【错解分析】本题主要考查对数函数的单调性及复合函数的单调性判断方法,在解题过程中易忽略对数函数的真数大于零这个限制条件而导致a的范围扩大。
【正解】函数
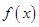 是由
是由 和
和 复合而成的,根据复合函数的单调性的判断方法
复合而成的,根据复合函数的单调性的判断方法(1)当a>1时,若使
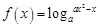 在
在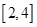 上是增函数,则
上是增函数,则 在
在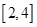 上是增函数且大于零。故有
上是增函数且大于零。故有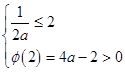 解得a>1。
解得a>1。(2)当a<1时若使
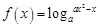 在
在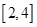 上是增函数,则
上是增函数,则 在
在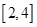 上是减函数且大于零。
上是减函数且大于零。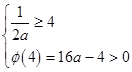 不等式组无解。
不等式组无解。综上所述存在实数a>1使得函数
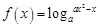 在
在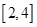 上是增函数
上是增函数【点评】要熟练掌握常用初等函数的单调性如:一次函数的单调性取决于一次项系数的符号,二次函数的单调性决定于二次项系数的符号及对称轴的位置,指数函数、对数函数的单调性决定于其底数的范围(大于1还是小于1),特别在解决涉及指、对复合函数的单调性问题时要树立分类讨论的数学思想(对数型函数还要注意定义域的限制)。

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
 是
是 上的偶函数,满足
上的偶函数,满足 ,当
,当 时,
时, ,则( )
,则( ) B.
B.
 D.
D.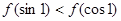
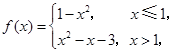 则
则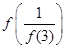 的值为
的值为  ,且
,且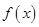 在
在 处取得极值.
处取得极值. 的值;
的值;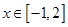 时,
时,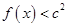 恒成立,求
恒成立,求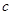 的取值范围;
的取值范围;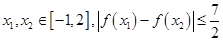 是否恒成立?如果成立,给出证明,如果不成立,请说明理由.
是否恒成立?如果成立,给出证明,如果不成立,请说明理由.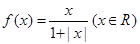 时,分别给出下面几个结论:
时,分别给出下面几个结论: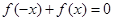 对
对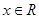 恒成立; ②函数
恒成立; ②函数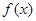 的值域为
的值域为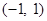 ;
;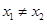 ,则一定有
,则一定有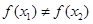 ; ④函数
; ④函数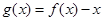 在
在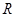 上有三个零点。 其中正确结论的序号有____________.
上有三个零点。 其中正确结论的序号有____________.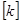 ,即
,即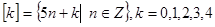 给出四个结论:
给出四个结论: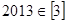 ,②
,②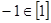 ,③
,③ ,④整数
,④整数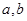 属于同一“类”,当且仅当是
属于同一“类”,当且仅当是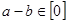 ,其中正确结论的个数是( )
,其中正确结论的个数是( )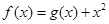 ,曲线
,曲线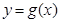 在点
在点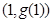 处的切线方程为
处的切线方程为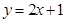 ,则曲线
,则曲线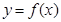 在点
在点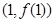 处切线的斜率为 ( )
处切线的斜率为 ( )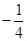
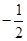
 已知函数
已知函数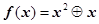 ,则
,则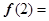 .
.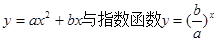 的图象只可能是 ( )
的图象只可能是 ( )