题目内容
已知f（x）（x∈R，且x≠kπ+
（k∈Z））是周期为π的函数，当x∈（-
，
）时，f（x）=2x+cosx．设a=f（-1），b=f（-2），c=f（-3）则（ ）
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| A．c＜b＜a | B．b＜c＜a | C．c＜a＜b | D．a＜c＜b |
已知f（x）（x∈R，且x≠kπ+
（k∈Z））是周期为π的函数，当x∈（-
，
）时，f（x）=2x+cosx，
故f′（x）=2-sinx＞0，故函数f（x）在∈（-
，
）上是增函数．
再由 a=f（-1），b=f（-2）=f（π-2），c=f（-3）=f（π-3），且π-2＞π-3＞-1，
可得 b＞c＞a，
故选D．
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
故f′（x）=2-sinx＞0，故函数f（x）在∈（-
| π |
| 2 |
| π |
| 2 |
再由 a=f（-1），b=f（-2）=f（π-2），c=f（-3）=f（π-3），且π-2＞π-3＞-1，
可得 b＞c＞a，
故选D．
练习册系列答案
阅读快车系列答案
相关题目
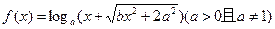是奇函数，则实数对
_______
，
，
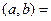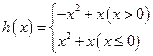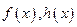的奇偶性依次为（ ）
是定义在[-1，1]上的偶函数，
的图象与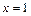
对称，且当x∈[ 2，3 ] 时，
222233．（1）求
上为增函数，求
的取值范围；（3）是否存在正整数
上？若存在，求出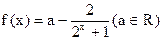
为奇函数（Ⅰ）求
的值；（Ⅱ）用函数单调性定义及指数函数性质证明: 
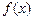在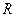
上是增函数。