题目内容
【题目】已知函数f（x）= 
cos4x+2sinxcosx﹣ sin4x．
（1）当x∈[0， 
]时，求f（x）的最大值、最小值以及取得最值时的x值；
（2）设g（x）=3﹣2m+mcos（2x﹣ 
）（m＞0），若对于任意x1∈[0， 
]，都存在x2∈[0， ]，使得f（x1）=g（x2）成立，求实数m的取值范围．
【答案】
（1）解： 
∵ 
∴ 
∴ 
，f（x）max=2∴ 
， 
综上所述： 
，f（x）max=2； 
，
（2）解：∵ 
∴ 
，∴ 
即f（x1）∈[1，2]，
，∴ 
，∴ 
，
又∵m＞0，∴ 
因为对于任意 
，都存在 
，使得f（x1）=g（x2）成立
∴ 
，
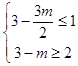∴m∈Φ
【解析】（1）利用两角和与差的三角函数化简函数的解析式，通过x的范围，结合正弦函数的有界性求解即可．（2）通过任意x1∈[0， 
]，存在x2∈[0， ]，求出两个函数的值域，列出不等式组 
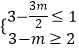，求解m的范围即可．
【考点精析】认真审题，首先需要了解三角函数的最值(函数
，当
时，取得最小值为
；当
时，取得最大值为
，则
，
，
)．
练习册系列答案
相关题目
【题目】春节是旅游消费旺季，某大型商场通过对春节前后20天的调查，得到部分日经济收入Q与这20天中的第x天（x∈N+）的部分数据如表：
天数x（天） | 3 | 5 | 7 | 9 | 11 | 13 | 15 |
日经济收入Q（万元） | 154 | 180 | 198 | 208 | 210 | 204 | 190 |
（1）根据表中数据，结合函数图象的性质，从下列函数模型中选取一个最恰当的函数模型描述Q与x的变化关系，只需说明理由，不用证明． ①Q=ax+b，②Q=﹣x2+ax+b，③Q=ax+b，④Q=b+logax．
（2）结合表中的数据，根据你选择的函数模型，求出该函数的解析式，并确定日经济收入最高的是第几天；并求出这个最高值．
