Question

【题目】如图，在平面直角坐标系中，锐角α和钝角β的终边分别与单位圆交于A，B两点．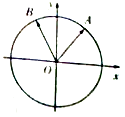
（I）若A，B两点的纵会标分别为 的值；
（II）已知点C是单位圆上的一点，且 的夹角θ．

Answer 1

【答案】解：（I）根据三角函数的定义，得sinα= ，sinβ= ．由α是锐角，所以，cosα= ．

由β为钝角可得 cosβ=﹣ ．

所以，cos（β﹣α）=cosβcosα+sinβsinα=（﹣ ）× + = ．

（II）已知点C是单位圆上的一点，且 ， ，

设 的夹角为θ，0≤θ≤π，则有 = ．

展开化简可得 =﹣ ．

可得cos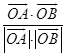θ= = =﹣ ，从而可得 θ= ．

【解析】（I）根据三角函数的定义，求得sinα= ，sinβ= ．由α是锐角、β为钝角可得cosα、cosβ的值，利用两角和与差的余弦公式求得cos（β﹣α）=cosβcosα+sinβsinα的值．

（II）由题意可得 ，设 的夹角为θ，0≤θ≤π，则有 = ．求出 的值，再利用两个向量的夹角公式求出cosθ，可得θ的值．

【考点精析】关于本题考查的两角和与差的余弦公式，需要了解两角和与差的余弦公式：才能得出正确答案．